いいこと思いついた。たいぶいいこと思いついた。NK風証明図のストリング図による描画で、けっこう困るのが選言〈論理OR〉の処理。これの描画法を思いついた。
思いついた時系列に沿って説明する。分配法則 A∧(B∨C) ⇒ A∧B ∨ A∧C (シーケント矢印は二重矢印)の証明を、上から下方向のストリング図で描く。
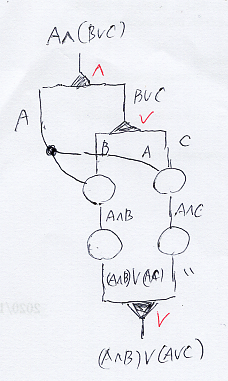
ここで、黒三角(▲、▼)は分岐と合流だが、AND分岐、AND合流、OR分岐、OR合流がある。
- AND分岐:命題を2つの成分命題に分ける。コピー〈対角〉と 連言のelim-left, elim-rightで作れる。
- AND合流:仮定が同じときだけ合流できて、デカルトペアを作る。
- OR分岐: 命題を2つの成分命題に分ける。場合分け、case文になる。
- OR合流: 結論が同じときだけ合流できて、デカルトコペアを作る。
AND分岐した2本のワイヤーは連言関係にあり、OR分岐した2本のワイヤーは選言関係にある。が、ワイヤーのあいだの領域が無色だと区別が付かない。領域色付きストリング図が必要になる。
領域色付きストリング図を避けるために、選言ボックスを導入する。
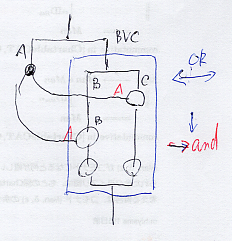
青い枠で囲っている部分が選言ボックス〈disjunction box〉。
- 選言ボックス内の分岐(▲)は選言分岐=場合分けである。
- 選言ボックス内の合流(▼)は選言合流であり、デカルトコペアを作る。
- 選言ボックス内の平行ワイヤーは選言関係にある。
- 選言ボックス内に横方向から入るワイヤーは連言〈AND〉でノードに入る。
選言ボックス内のノードは、縦方向に上から入るワイヤーと横方向に左から入るワイヤーを持つ。
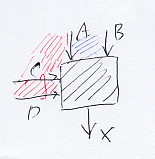
選言ボックス内で特有のこのテのノードを二面ノード〈two-face node〉と呼ぶ。上の図で、AとBは選言関係にありノードに入る。CとDは連言関係にありノードに入る。上のワイヤー達〈ケーブル〉と左のワイヤー達〈ケーブル〉は選言関係にある。入力全体は、(C∧D)∧(A∨B)、カンマを使って書くと C∧D, A∨B 。あるいは、
- C,D → ↓A | B ⇒ X
次は雑多なことを描いた図。
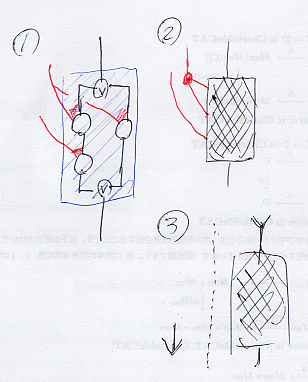
(1)は選言ボックスそのもの、(2)は選言ボックスをブラックボックス化。選言ボックス自体が二面ノードになることがわかる。ただし、選言ボックスの入力は1本、出力も1本に限定する。横からの入力は自由に入っていいとする。その意味で、選言ボックスは、連言環境に置かれた特殊な二面ノードということになる。
(3)は、自然演繹証明図で選言ボックスをどう処理するかを描いている。選言ボックスの入力端を左に、それとは別に選言ボックスを右に書いて、結合〈composition〉するタクティク〈リーズニング{オペレータ | コンビネータ}〉で組み立てる。
次の図は、ボックスを使わずに色付きストリング図で分配法則の本質的部分を描いた図。
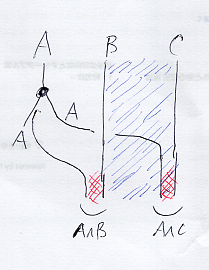
ここでまた用語の整理をしておく。
| 圏論 | 檜山 | Lean | 論理 |
|---|---|---|---|
| 対象 | 論理式 | 命題 | 論理式 |
| 生成射 | 原子証明 | ルール | 推論ルール |
| 射 | 証明図 | 証明{項 or 式} | 証明図(N*) |
| 雑多な生成的モノ | リーズニングオペレータ | タクティク | 推論ルール |
| 雑多なモノ | リーズニング図 | {{タクティク}?{スクリプト}?}! | 証明図(L*) |
- タクティクスクリプトは、基本〈原子 | 組み込み〉タクティクとタクティクコンビネータで作る。タクティクスクリプト言語はDSLなプログラミング言語。タクティク作成言語はまた別なプログラミング言語(LeanではLean自身)。
- シーケント証明図=リーズニング図はツリー。そのツリーを深さ優先再帰的順序でトラバースしてシリアライゼーションしたのが単純順次タクティクスクリプト。
選言ボックスは選言消去に対応する。となると、存在消去もボックスで描けるだろう。含意導入がワイヤーベンディングだから、全称導入もワイヤーベンディングなのか? ちょっと違う気もする。圏論的双対性と有限・無限との対比で考えよう、っと。