選言ボックスと二面ノード - (新) 檜山正幸のキマイラ飼育記 メモ編 の続き。絵は裏写りがすごくて、ゴミが入っていたりする。
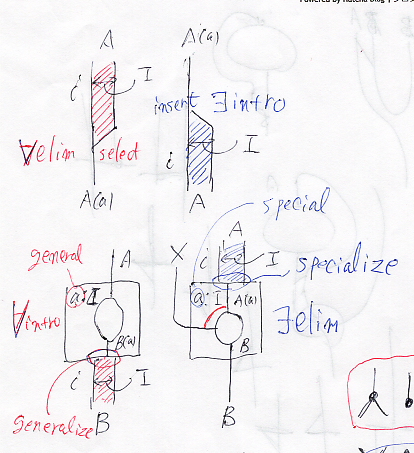
図の右下はゴミ(別な図の一部)。左から右、上から下の順で説明。
- ∀elim :
∀i∈I.A ⇒ A(a) (⇒はシーケント矢印)の証明。ケーブル(=ワイヤーの束)は連現環境のケーブル(論理式の無限かも知れないリスト=族)となる。連現環境は赤。複数のワイヤーから一本を選ぶ行為がセレクション。セレクションのときの特定特殊なインデックスがa。よって ∀i∈I.A から i = a とインデックスを特殊化して A(a) = Aa が得られる。
- ∃intro :
特定特殊なインデックスaに対して A(a) = Aa は成立している。選言環境内の複数のワイヤーの一員として A(a) を挿入〈インサーション〉する。ケーブルからのワイヤーセレクションと、ケーブルへのワイヤーインサーションが双対。セレクション元のケーブルは連言ケーブル。インサーション先のケーブルは選言ケーブル。ケーブルの“幅”がインデキシングセット=論域。
- ∀intro :
全称導入の推論〈証明構成 | リーズニング〉は、全称ボックスで行う。全称ボックス先頭で宣言された変数〈インデックス〉は{一般 | 任意}{変数 | インデックス}。インデックスセット〈論域〉I内の任意の要素を表す。AからB(a)に至る証明があるとき、全称ボックスの出口で一般化〈generalize〉して、全称命題をボックスの外に出力してよい。
入力として明示された命題 A 以外に、ボックス外の命題を自由に使ってよい。あるいは、明示的入力に付け加えてもよい。
- ∃elim :
存在消去の推論〈証明構成 | リーズニング〉は、存在ボックスで行う。存在ボックス先頭で宣言された変数〈インデックス〉は{特殊 | 選択}{変数 | インデックス}。インデックスセット〈論域〉I内の特定特殊な要素を表す。存在ボックスの入り口で選択的な特殊化〈specialize | 選択〉して A(a) を作る。A(a)からBに至る証明があるとき、そのまま存在ボックスをから出力してよい。
入力として明示された命題 A 以外に、ボックス外の命題を自由に使ってよい。しかし、明示的入力に付け加えることは出来ない。
次のような双対性がある。
- ワイヤーセレクション ←→ ワイヤーインサーション
- 連言ケーブル ←→ 選言ケーブル
- 全称導入ボックス ←→ 存在消去ボックス
- 一般変数 ←→ 特殊変数
- 一般化退出 ←→ 特殊化進入
次の図は、連言ボックスと選言ボックス:
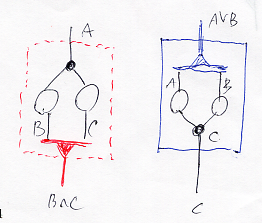
連言ボックスが点線なのは、外部の環境がそもそも連言環境なのでボックスを作る意味がないから。一方、選言ボックスは明示的に作って内部を選言環境にする。選言環境内へも連言的入力を自由に入れて良い。ただし、絵では左横から。
次のような双対性がある。
- 連言ボックス ←→ 選言ボックス
- 対角〈コピー〉 ←→ 余対角
- デカルトペア ←→ デカルトコペア
- 連言合流 ←→ 選言分岐
連言環境、選言環境で使えるジャンクション。
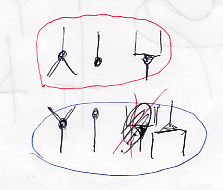
- 対角〈コピー〉 ←→ 余対角
- 削除 ←→ 生成
- 合流 ←→ 分岐
- 真不可視ワイヤー ←→ 偽不可視ワイヤー
連言/選言ボックスと全称/存在ボックスの対応は:
- 対角 ←→ 一般変数導入 全称限量消去
- 連言合流 ←→ 総称限量退出
- 選言分岐 ←→ 特殊変数導入
- 余対角 ←→ 存在限量消去、退出
あとは、含意の導入消去をパイ型構成と共に徹底的に考えればいいかな。