データ従属性

本編ネタ

$`\newcommand{\mrm}[1]{\mathrm{#1} }
\newcommand{\mvto}{ \twoheadrightarrow }
\newcommand{\Iff}{\Leftrightarrow}
\newcommand{\Imp}{\Rightarrow}
`$

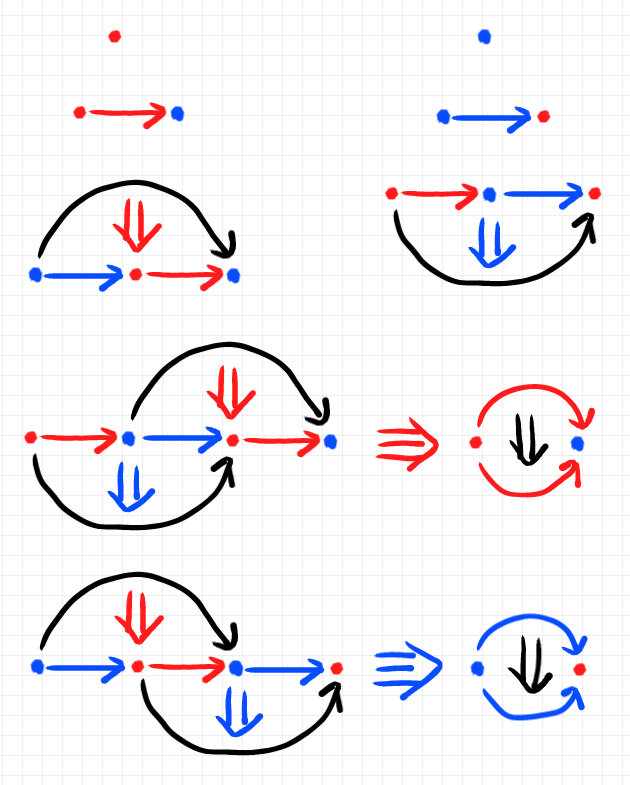
関数従属性

$`\mrm{FD}(X\to Y)(R) :\Iff \\
\quad \forall t_1, t_1 \in R. \,
t_1[X] = t_2[X] \Imp t_1[Y] = t_2[Y]
`$

言い換えると：

$`\mrm{FD}(X\to Y)(R) :\Iff \\
\quad \vec{R}:R[X] \to R[Y] \text{ is-a function}
`$

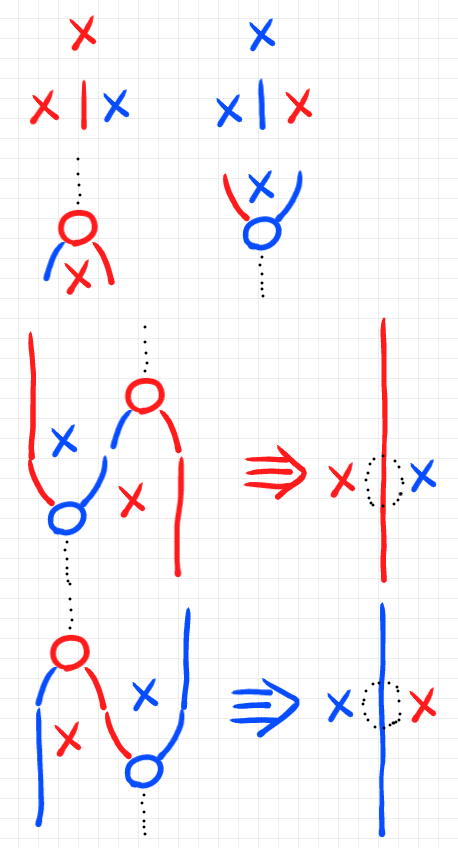
多値従属性

$`\text{When }X\cap Y = \emptyset\\
\mrm{MVD}(X \mvto Y)(R) :\Iff\\
\quad \forall t_1, t_2 \in R.\,
t_1[XY] = t_2[XY] \Imp\\
\qquad \exists t \in R. t[XY] = t_1[XY] \land t[X(R - XY)] = t_2[X(R - XY)]
`$

言い換えると：

$`\text{Whe }X, Y, Z \text{ mutually disjoint}\\
\mrm{MVD}(X \mvto Y)(R) :\Iff\\
\quad \forall t_1, t_2 \in R.
t_1[XY] = t_2[XY] \Imp\\
\qquad \exists t \in R. t[XY] = t_1[XY] \land t[XZ] = t_2[XZ]
`$

データベースの例

具体例 本編ネタ

http://webdam.inria.fr/Alice/pdfs/Chapter-8.pdf より。

Movieテーブル

  • title
  • Director
  • Actor

Showing〈上映〉テーブル

  • theater
  • screen
  • title
  • snack ： 提供しているスナック（飲料と軽食）

昔は2本立てがあったが、今はほぼない。

以前から使っている。

学生テーブル

  • 学生番号
  • 性
  • 名
  • 生年月日
  • 学年

教員テーブル

  • 教員番号
  • 性
  • 名
  • 生年月日

研究室テーブル

  • 名前
  • 主任教員

科目テーブル

  • タイトル
  • 年度
  • 担当教員
  • 教室

履修テーブル

  • 学生
  • タイトル
  • 年度

教科書テーブル

  • タイトル
  • 年度
  • 本
  • 種別

本テーブル

  • (略)

プリンター

メモ pc-setup
全般的なこと
  • 用途： ドキュメント印刷 vs.写真印刷
  • 方式：インクジェット、レーザー（業務用ドキュメント向け）
  • インク： 染料インク（写真向け）、顔料インク（ドキュメント向け）
  • 基本色シアン、マゼンタ、イエローが染料インク、
  • ブラックは、染料インクと顔料インクがある。文字用ブラックが顔料インク。
  • フォトブルーやグレーが入ると色品質が上がるが、ドキュメントではあんまり関係ない。4色でも十分。
  • 大容量タイプはドキュメント向きでランニングコストがおさえられる。
  • エプソンは写真指向で文字が苦手ぎみ
  • ブラザーは文字印刷指向、速度が安定している。平均的に速め。インク代安い。が、大容量タイプには勝てない。
  • 候補：ブラザー DCP-J926NW
  • 候補：キャノンG3360 背面給紙だ、G6030
  • 候補： ブラザー J526N
  • エコタンクモデルは印刷速度が遅いのが欠点
  • キャノン ピクサス TS8430 既存とほぼ同じ。TS7530もあるが在庫なしかも。
要求仕様
  • (幅x高さx奥行き) 横幅 450mm程度、高さ任意、奥行き 370mm以内
  • 質量 8kg程度
  • 前面給紙カートリッジ
Notion AIのおすすめ。
  • エプソン PX-M884F
  • キャノン PIXUS TR7530
  • ブラザー MFC-J6975CDW

これらのプリンターは、ランニングコストが比較的安く、文書印刷に適しています。また、前面カートリッジ方式を採用しているため、使い勝手も良いです。予算の範囲内で購入できるので、ぜひ参考にしてみてください。

役に立たん。

Youtubeを2倍速スキップで見た。

業務用の話。既存ブラザープリンターのランニングコストが高い、と。A3エコタンク方式の エプソン EW-M 5610 FT に買い替え。カラー 9ipm、デカイやつであまり参考にならん。

2年前、エプソンから Canon G3360 への買い替え。やはりランニングコストが問題意識。初期化オペレーションの参考にはなる。価格.com は https://kakaku.com/item/K0001307400/ モノクロ約0.4円（税別）、カラー約0.9円（税別）。型落ちでも値下がりなく、3万超えてる。USB接続。背面給紙のみ、ダメだ。

2週間前 Canon G3370 。これも、インク代、ランニングコストが問題意識。価格.comは https://kakaku.com/item/J0000039972/ モノクロ約0.4円（税込）、カラー約1.0円（税込）、価格は3万くらい。これも背面給紙のみ、ダメだ。 前面給紙カートリッジがない。カラー 6ipm。前面給紙ならよかったのだが、、、

1年前、Canon XK100 。ハイスペックモデル。6色と5色の差はさほどない。これはオーバースペックだな。ランニングコストは抜群に安い。価格.com https://kakaku.com/item/K0001389158/ 9.8円/p エプソンは遅い。TS6330 もオススメとのこと（次項）。

2年前（2021/03/13）TS6330 ランニングコスト高い。価格.com https://kakaku.com/item/J0000031067/ 19円/p

2022/08/28 CANON XK500 5万円。6色いらん。写真用だし、オーバースペック。

2019/12/20 CANON G6030 業務用。インク代、安い。前面カートリッジ。価格.com https://kakaku.com/item/K0001160573/ ランニングコストは抜群ではあるが。

2023/05/06 ブラザー DCP L2550DW 価格.com は https://kakaku.com/item/K0001049724/、確かに安い。10.35kg 。モノクロ、消耗品ビジネス。ダメだ。紙ロット500枚は入らない。WPS非対応、「WPS」はググれ。

ブラザーDCP-J4140N 価格.com https://kakaku.com/item/K0001371950/ 。3万円くらい。エコタンク方式。横幅44cm。前面カートリッジ。12.5 円/p

EPSONエコタンクプリンタEW-M571T がダメだっていう話。価格.com https://kakaku.com/item/K0000991693/ 6.5 円/p

2021/11/26 Brother DCP-J926N 前面用紙カートリッジ。けっこういいかも。2万円台。両面印刷はないはOK。価格.con https://kakaku.com/item/J0000036257/ 23.1 円/p

2020/03/16 キャノン Ｇ7030 FAXとか要らない。価格.com https://kakaku.com/item/K0001184802/ 前面カートリッジ、ギガタンク仕様。

その他
追加

2019/03/01 キャノン G1310 プリンタ単体モデル。対応する複合機は G3310。タンク方式。うるさい（別にいい）。最大給紙100枚（少ない）。Windowsのみ。プリンタのみも良いような気がする。

2021/01/25 5分30秒くらい：タンク方式で元が取れるのは、3,4千枚くらい印刷した時点、という話。

メタ巡回性、自己言及、非可述性、手塚治虫、火の鳥

画像 リンク 本編ネタ

画像：

*1

*2



*3

リンクと引用：

https://tezukaosamu.net/jp/manga/399.html より：

猿田博士が暮らすスノーグローブのような半球状のドームは、生命を封じ込めたグローブ=地球そのものを暗示するものとして、作品のテーマを見事に視覚化していると言えるでしょう。

松浦だるまさんへのインタビュー記事 (https://tezukaosamu.net/jp/mushi/entry/13243.html) より：

どういうところにショックを受けたのでしょうか。


松浦 　 『火の鳥』未来編の、極大から極小へ行くシーンです。時間や空間を超えて、宇宙という大きな世界をみせた後にミクロの世界を見せて、生物の細胞から宇宙まですべて生きものなんだ、と火の鳥に教えられるシーンなのですが、あのシーン、完全に自分がなくなったんですよね。

*1:画像は https://www.amazon.co.jp/dp/B00006II9F より

*2:バエズ〈John C. Baez〉が説明に使っていたが、出典不明

*3:画像： https://tezukaosamu.net/jp/mushi/entry/13243.html より

型理論の基本概念のリンク

[CTRL]+クリック

全称変数と特称変数

半形式証明スクリプト 論理 Lean

全称変数は、型宣言された変数で、その型の任意のモノを表す。任意変数と言ってもいい。$`\require{color}
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }
\newcommand{\for}{\Keyword{for } }
\newcommand{\assume}{\Keyword{assume } }
\newcommand{\consider}{\Keyword{consider } }
\newcommand{\st}{\Keyword{ st } }
\newcommand{\endBlock}{\Keyword{end } }
`$

$`\for x : X`$

または、

$`\assume x : X\\
\quad \cdots\\
\endBlock
`$

で全称変数が導入される。$`\for`$で導入された変数のスコープはすぐ外のブロックの終了まで。$`\assume`$は自分のブロックを作る。

それに対して特称変数は条件と共に導入される。

$`\consider x : X \st P(x)\\
\quad \cdots\\
\endBlock
`$

全称変数／特称変数は、ブロックに閉じ込められたスコープ付き変数〈scoped variable〉で、スコープ外に漏れることはない。外のスコープの名前をシャドーするが、通常はシャドーしないように使う。

全称変数は、対応する全称束縛変数に閉じ込めてスコープからoutgoingできる。逆に、存在束縛変数は、特称変数としてスコープ内にincommingできる。

全称変数は、スコープ内で自由変数として使ってよく、特称変数は条件を満たす定数のように使ってよい。

  • Lean 4で、全称変数の生成は、variable宣言、関数引数、assume〈ラムダ変数〉で行う。
  • Lean 4で、特称変数のサポートがほとんど無いようだ。これがネックになっている。

タクティクに関する引用

半形式証明スクリプト 論理 リンク 本編ネタ

ブラケットは檜山が挿入。

a [tactic] proof is a more or less structured sequence of commands that manipulate an implicit proof state. Thus the proof text is only suitable for the machine; for a human, the proof only comes alive when he can see the state changes caused by the stepwise execution of the commands. Such proofs are like uncommented assembly language programs.

Despite decades of research on automation and proof assistants, writing formal proofs remains arduous and only accessible to a few experts.

arduous ： つらい

半形式証明の良い事例 (2)

半形式証明スクリプト リンク 具体例

$`\newcommand{\mrm}[1]{\mathrm{#1}}
\require{color}
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }
\newcommand{\letsShow}{\Keyword{lets show } }
\newcommand{\conclude}{\Keyword{conclude } }
\newcommand{\par}{\Keyword{par } }
\newcommand{\endBlock}{\Keyword{end } }
\newcommand{\case}{\Keyword{case } }
\newcommand{\assume}{\Keyword{assume } }
\newcommand{\consider}{\Keyword{consider } }
\newcommand{\suchThat}{\Keyword{such that } }
\newcommand{\curs}{ \textcolor{orange}{\blacksquare} }
\newcommand{\Imp}{ \Rightarrow }`$
ヤシコフスキ〈Stanisław Jaśkowski〉／カリシュ〈Donald Kalish〉／モンタギュー〈Richard Montague〉〈JKM〉形式の証明：

$`\letsShow ( (p \Imp q) \land (\lnot r \Imp \lnot q) )\Imp (p \Imp r)\\
\bullet (p \Imp q) \land (\lnot r \Imp \lnot q) \text{ を仮定して、 } (p \Imp r) \text{ を導く}\\
\quad \assume (p \Imp q) \land (\lnot r \Imp \lnot q) \:\cdots \text{(1)}\\
\qquad \letsShow p \Imp r\\
\qquad \bullet p \text{ を仮定して }r \text{ を導く}\\
\qquad\quad \assume p \:\cdots \text{(2)}\\
\qquad\qquad \downarrow \text{上の仮定を再掲}\\
\qquad\qquad (p \Imp q) \land (\lnot r \Imp \lnot q) \:\cdots \text{(3)}\\
\qquad\qquad \downarrow \text{すぐ上の連言の左側}\\
\qquad\qquad (p \Imp q) \:\cdots \text{(4)}\\
\qquad\qquad \downarrow \text{モーダスポネンスを適用}\\
\qquad\qquad q \:\cdots \text{(5)}\\
\qquad\qquad \downarrow \text{上の連言の右側}\\
\qquad\qquad \lnot r \Imp \lnot q \:\cdots \text{(6)}\\
\qquad\qquad \letsShow r\\
\qquad\qquad \bullet \text{背理法を使う}\\
\qquad\qquad\quad \assume \lnot r \:\cdots \text{(7)}\\
\qquad\qquad\qquad \downarrow\text{先の命題を再掲}\\
\qquad\qquad\qquad \lnot r \Imp \lnot q \:\cdots \text{(8)}\\
\qquad\qquad\qquad \downarrow \text{モーダスポネンスを適用}\\
\qquad\qquad\qquad \lnot q \:\cdots \text{(9)}\\
\qquad\qquad\qquad \downarrow\text{先に得られた命題を再掲}\\
\qquad\qquad\qquad q \:\cdots \text{(10)}\\
\qquad\qquad\qquad \downarrow\text{矛盾が生じる}\\
\qquad\qquad\qquad \bot\\
\qquad\qquad\quad \endBlock\\
\qquad\qquad \conclude r\\
\qquad\quad \endBlock\\
\qquad \conclude p \Imp r\\
\quad \endBlock\\
\conclude ( (p \Imp q) \land (\lnot r \Imp \lnot q) )\Imp (p \Imp r)
`$

インデントガイドラインがあったほうがよい。

※ カリシュ／モンタギューの教科書は "Logic: Techniques of Formal Reasoning"

半形式証明の良い事例

半形式証明スクリプト リンク 具体例

structured calculational proof に関するフォーマットの提案。論理としては別になんてことないが、半形式証明スクリプトの構文としては参考になる。$`\newcommand{\mrm}[1]{\mathrm{#1}}
\require{color}
\newcommand{\Keyword}[1]{ \textcolor{green}{\text{#1}} }
\newcommand{\calc}{\Keyword{calc } }
\newcommand{\endcalc}{\Keyword{end } }
\newcommand{\theorem}{\Keyword{theorem } }
`$

  • Mizar / Andrzej Trybulec (1973～現役)
  • Isabelle / Lawrence Paulson (1986～現役)
  • Coq / Thierry Coquand, Gérard Huet (1989～現役)

サンプル：

$`\theorem \text{sample } (k : \mrm{Nat}) : \mrm{even} ( k^3 + k) :=\\
\calc \\
\mrm{even} ( k^3 + k)\\
\updownarrow //\text{ Extract the common factor.}\\
\mrm{even} (k\cdot (k^2 + 1) ) \\
\updownarrow //\text{ Distribute even over }\cdot \text{ .}\\
\mrm{even}(k) \lor \mrm{even}(k^2 + 1) \\
\updownarrow //\text{ Simplify the right disjunct.}\\
\quad \calc \\
\quad \lnot \mrm{even}(k^2 + 1)\\
\quad \updownarrow //\text{ Since }\mrm{even}(i + 1) \text{ is }\lnot \mrm{even}(i)\\
\quad \lnot \mrm{even}(k^2 )\\
\quad \updownarrow //\text{ The defiition of square}\\
\quad \lnot \mrm{even}(k \cdot k )\\
\quad \updownarrow //\text{ Distribute }\mrm{even} \text{ over }\cdot \text{ .}\\
\quad \lnot (\mrm{even}(k)\lor \mrm{even}(k))\\
\quad \updownarrow //\text{ Disjunction is idempotent.}\\
\quad \lnot \mrm{even}(k)\\
\quad \endcalc\\
\mrm{even}(k) \lor \lnot\mrm{even}(k)\\
\updownarrow //\text{ The law of the excluded middle.}\\
\top\\
\endcalc`$

曖昧表現、一様化、同一視

Lean 論理 多義語 教育

曖昧表現は：

  1. 名前・記号の借用 例： G = (G, *, 1)
  2. 省略 例： G = (G, *)
  3. 名前・記号の多義的使用〈オーバーロード〉

曖昧表現の解決は、データベース検索。検索条件はパターンマッチ問題〈ユニフィケーション問題〉となる。パターンマッチ問題を解いて曖昧表現を解決する。データベース検索には次の種類がある。

  1. 一意検索： 結果が一意的でないと失敗。
  2. 候補検索： 結果があれば成功、ないと失敗。
  3. 選択検索： 結果があると適当に一個選ぶ。ないと失敗。

検索は、名前空間構造と密接に関係している。基本はコアージョン・データベースで、コアージョン・データベースの一部に増強データベース〈インスタンス・データベース〉がある。コアージョンは型変換子だが、型変換子のデータベースへの登録は、アドホック登録とパラメトリック登録がある。

曖昧表現の利用と解決は本来の構造記述とは独立で自由に導入・削除ができるべき。

一様化の例として、総称引数 < >、インデックス引数 [ ]、通常引数を全部同等に扱うこと。

同一視の例として、カリー同型による同一視、自明指数同型（A ≒ A^1）による同一視、左右の単位律子による同一視などがある。証明無関心〈proof irrelevance〉も同一視。

様々な計算系と混乱

Lean 論理 半形式証明スクリプト 教育

次の計算系がある。

計算対象物 CC圏 CC複圏 CC多圏
（広義）射 ◯ ◯ ◯
コンビネータ △ ◯ ◯
アレンジメント △ ◯ ◯
  • CCは Cartesian Closed
  • ◯：うまく定式化できる。
  • △：ある程度は定式化できる。

演算：

  • 射に対して： 結合、直積、カリー化、評価
  • コンビネータに対して： 結合、直積、（カリー化：あまりやらない）
  • アレンジメントに対して： ジョイン、併置

埋め込み：

  • 射を単純複射として埋め込む。
  • 複射の並びをクローン多射として埋め込む

結局はCC多圏での計算が一番便利。

新しいキーワード

教育 論理 半形式証明スクリプト
  • lambda ： ラムダ抽象 assume
  • backlog ： バックログラムダ抽象 postulate / demand 要請、ラムダ抽象だがバックログだとマークする。ラムダ変数はバックログ変数＝スタブ＝ダミー。
  • prepare ： 引数の準備
  • next ： 区切り記号
  • and_also ： 区切り記号
  • end ： 終端記号
prepare
 A1 := α1
 ...
 An := αn
let x:B := β
...

展開形

let _1 : A1 := α1
 ...
let _n: An := αn
let x:B := β _1 ... _n
...

returnのとき：

prepare
 A1 := α1
 ...
 An := αn
return β : B end

展開形

let _1 : A1 := α1
 ...
let _n: An := αn
return (β _1 ... _n : B) end