2022-08-09

シーケントの用語

論理半形式証明スクリプト多義語

とある論文で使っていた用語法：

シーケントの左辺＝ antecedent〈前件〉
シーケントの右辺＝ succedent〈後件〉
イニシャルシーケント＝公理シーケント

シーケントの推論規則用語：

上式＝ premises〈仮定〉
下式＝ conclusion〈結論〉

前件、後件、仮定、結論をどのレベルに割り当てるかは人それぞれ。致し方ない。

一般に、矢印で区切られた順序対に関しては、次が良いと思う。

矢印の根本側： pre-item
矢印の先端側： post-item

2022-08-06

双対的な概念

論理半形式証明スクリプト

保証〈warranty〉： derivation T → A
反駁〈refutation〉： derivation A → ⊥
証拠〈witness〉：存在記号導入に使う要素、項
事例〈instance〉：全称記号消去に使う要素、項
存在スタート条件〈existential starting condition〉：存在記号消去に伴う開始時条件
全称エンド条件〈universal ending condition〉：全称記号導入に伴う終了時条件
存在変数〈existential variable〉：存在記号消去に伴う型付き変数
全称変数〈universal variable〉：全称記号導入に伴う型付き変数

次の双対性がある。

保証 ←→ 反駁
証拠 ←→ 事例
存在スタート条件 ←→ 全称エンド条件
存在変数 ←→ 全称変数

存在と全称の双対性は、存在ボックスと全称ボックスの双対性。

2022-08-06

帰納的に構成される型

論理型理論

data Tree a
  = Leaf a
  | Tree (Tree a) (Tree a)

値コンストラクタ、型コンストラクタ、型が紛らわしいという例。値コンストラクタをタグだと考えると：

type Tree<A> =
 @Leaf A | @Tree [Tree<A>, Tree<A>]

タグ @Leaf, @Tree に対応する値コンストラクタを ^Leaf, ^Tree とすると：

^Leaf<A> : A → Tree<A>
^Tree<A> : Tree<A>×Tree<A> → Tree<A>

これで区別できた。

@Tree ：タグ
^Tree ：タグが定義する値コンストラクタ写像 ^Tree<A>(s, t) = @Tree [s, t]
Tree ：タグ／値コンストラクタで帰納的に定義される型コンストラクタ Tree:Type → Type

2022-08-06

バンチ書き換え

論理教育半形式証明スクリプト

対象物：

型
関数
値〈データ | ポイント〉特別な関数
汎関数〈メタ関数〉
命題（真偽値、述語、論理式）
導出
保証特別な導出
リーズニング〈メタ導出〉

カリー／ハワード／ランベック対応

型	命題
関数	導出
値	保証
汎関数	リーズニング

項：

型項（多くの場合は集合項）
関数項〈項〉
値項
汎関数項
命題項〈論理式〉
導出項〈証明項〉
保証項
リーズニング項

バンチと書き換えアクション：

型バンチと型構成子〈型コネクティブ〉
関数バンチと関数構成子〈関数コネクティブ〉
値バンチと値構成子〈値コネクティブ〉＝関数後結合主体
汎関数バンチと汎関数構成子〈汎関数コネクティブ〉
命題バンチと命題構成子〈論理コネクティブ〉
導出バンチと導出構成子〈導出コネクティブ〉
保証バンチと保証構成子〈保証コネクティブ〉＝導出後結合＋リーズニング
リーズニングバンチとリーズニング構成子〈リーズニングコネクティブ〉

構成スクリプト：

型構成スクリプト
関数構成スクリプト＝汎関数スクリプト
値構成スクリプト＝関数スクリプト
汎関数構成スクリプト
命題構成スクリプト＝導出スクリプト
導出構成スクリプト＝リーズニング・スクリプト
保証構成スクリプト＝導出スクリプト？

課題：スクリプトレベルでのカリー／ハワード／ランベック対応

2022-08-06

証明の意義

muses 論理教育

https://arxiv.org/abs/2102.03044 から。

証明が行うこと	読者の心に形成されるもの
guarantee	trust
explain	insight, understanding

2022-08-06

証明の同義語

論理多義語

https://arxiv.org/abs/2102.03044 の冒頭、同語義：

{mathematical | logical | rigorous | formal | rational}* {derivation | proof}

単なる多義語ならいいのだけど、実際には曖昧語になっているのがタチが悪い。

2022-08-06

バンチ書き換えの共通構造

半形式証明スクリプト論理

動詞 DoSomething	名詞 Something	短縮
construct	construction	cons
calculate	calculation	calc
derive	derivation	deriv
reason	reasoning	reas

Begin Something
  WeHave A
    And, B
  Using Something X params
  WeHave A'
    And, B'
  Using Something Y params
  ...
  ...
End Something

WeHave は省略可能。And, は単に , でもよい。その他省略すると：

Something
  A, B
  Using X params
  A', B'
  Using Y params
  ...
  ...
End

あるいは：

Something foo := Begin
  A, B
  Using X params
  A', B'
  Using Y params
  ...
  ...
End

2022-08-05

導出と置換の書き方

本編ネタ半形式証明スクリプト論理

$`\newcommand{\Sep}{\mathrel{\|} }
\newcommand{\Subst}[2]{ {\scriptsize \begin{bmatrix} #1\\ #2 \end{bmatrix} } }
%`$

$`\quad \alpha \Sep \varphi: \Gamma \to B`$

ここで：

型コンテキストはギリシャ文字小文字
命題コンテキストはギリシャ大文字
命題はラテン文字大文字
導出はギリシャ小文字後半

これは以下と同じ。

$`\quad \varphi: \Gamma \to B \text{ in }\mathrm{Prop}[\alpha]`$

$`f:\beta \to\alpha`$ を型コンテキストのあいだの多写像として、置換結果は次の導出になる。

$`\quad \beta \Sep \varphi': \Gamma\Subst{f(\vec{y})}{ \vec{x}} \to B\Subst{f(\vec{y})}{ \vec{x}} `$

2022-07-26

証明記述の例

本編ネタ半形式証明スクリプト論理画像

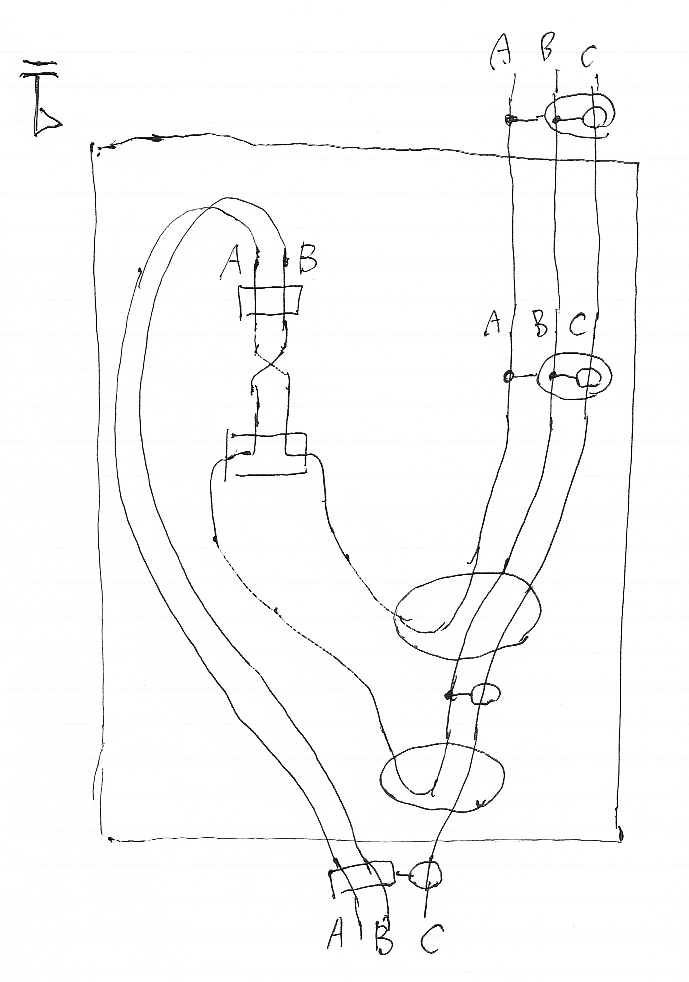
palette CCC {
  parameter wire X, Y, Z
  node left-eval[X, Y] : (X, X⇒Y) → (Y)
  node decomp-prod[X, Y] : (X×Y) → (X, Y)
  node swap[X, Y] : (X, Y) → (Y, X)

  action LeftCurry[X, Y, Z] ::
    ((X, Y) → (Z)) ~~→ ((Y) → (X⇒Y))

  // ...省略...

  parameter node f: X, Y → Z
  conversion Beta[X, Y, Z, f] ::
    ( (X, LeftCurry[X, Y, Z](f));left-eval[X, Y] ) ~~→ (f)

  // ...省略...

}

$`(X, X\Rightarrow Y) \to (Y)`$
$`( X\times Y) \to (X, Y)`$
$`(\, (X, Y) \to (Z)\,) \rightsquigarrow (\,(Y) \to (X \Rightarrow Y)\,)`$

alias ∧ := ×
declare A, B, C
canvas
  put A∧B, A⇒(B⇒C)
  put CCC.decomp-prod[A, B]
  put CCC.swap[A, B]
  put --after=1 CCC.left-eval[A, B⇒C] 
  put CCC.left-eval[B, C]
  we possess ( A∧B, A⇒(B⇒C) ) → (C)
close
exec CCC.LeftCurry[A∧B, A⇒(B⇒C), C]

2022-07-23

描画記述の基本

半形式証明スクリプト論理

描画モデルは、描画エージェント（一人、ペインター、画師、絵師）、キャンバス（入れ子可能）、パレット（複数可能）からなる。

唯一のカレントキャンバスを持つ。
唯一のカレントフォーカスポイントを持つ。それは、カレントキャンバス上の点。
カレントフォーカスポイントにより、カレントキャンバスは、不可視エリア（左）、描画済みエリア（上）、ブランクエリア（白紙）の3つのエリアに分割される。
anyway, by the way で左に新しいエリアが生成される。新しいエリアはブランクだけ。

次は基本的な概念：

キャンバス：有限矩形領域だが、下と左に自由に伸ばせる。
ポート（キャンバス境界線上にマークする）
ホール〈穴〉、またはホール〈穴〉マーク〈スロット〉、テンプレーティングで使う。
くり抜き hollow-out
はめ込み fill-in
差し替え replacement
フォーカスポイント：キャンバス上の点で、上が描画済み、左側は見えない。
視野〈field of vision | visible area | 可視領域〉左側は見えない。
セレクションボックス：特定のワイヤー達に注目して、その下に描く。他のワイヤーはセレクションボックスに入れない。
左遷移、anyway, by the way ：現在のフォーカスポイントをリターンポイントとして保存して、左側ブランクエリアのTopLeft にフォーカスポイントを移動する。
戻り遷移、go back ：直前に保存したリターンポイントにフォーカスポイントを設定する。
下端ワイヤー群：ビジブルなワイヤーで、下端でダングリングしているすべてのワイヤーの集合
セレクション：下端ワイヤー群の連続する一部を選んで、その他のワイヤーを一旦無視すること。close select でセレクションモードから抜ける。
視野変更：左遷移、戻り遷移、セレクション開始、セレクション終了で視野変更ができる。
デカルト・スパイダリング：コピー、破棄、スワップの繰り返し、rearrangeコマンドで実行する。
動的パレット： Bottomline は下端ワイヤーの集合。原則的に番号でアクセス。Diagram には単一の図のみが存在する。Bottomlineをhaveし、Diagramをpossessしている。
エリア移動：左エリアへの移動が anyway、セレクションエリアの生成と移動が select。左エリアから親エリアへの移動が go back、セレクションエリアを閉じて親エリアに戻るのが close select。

coloured properad, coloured PROP, many-sorted Lawvere theory の関係は https://arxiv.org/pdf/1512.05980.pdf で確認。

2022-07-23

型理論と論理のすり合わせ (3)

半形式証明スクリプト論理用語法

型・関数	命題・導出
0-射型	0-射命題
0-オペレータ積	0-オペレータ連言
0-オペレータ指数	0-オペレータ含意
0-射指数型	0-射含意命題
1-射関数	1-射導出
1-射データ	1-射保証〈ワランティー〉
1-射入射〈余射影〉	1-射証拠
1-射射影〈成分〉	1-射具体化
構造化型	構造化命題
複1-射複関数	複1-射複導出
多1-射多関数	多1-射多導出
ラムダ抽象	含意導入
評価写像	モーダスポネンス
0-射パイ型	0-射全称命題
	翻訳関手

保証〈ワランティー〉は新しく導入した言葉。

その他：

型コンテキスト＝構造化型
関数置換＝多関数
命題コンテキスト＝構造化命題

ただし、役割としての型コンテキスト、命題コンテキストは使うかも。

2022-07-22

型理論と論理のすり合わせ (2)

半形式証明スクリプト論理用語法

少し追記。

型コンテキストを型判断と呼ぶ用語法は採用しない。
型シーケント $`\Gamma \vdash M:\sigma`$ を型判断〈typing judgement〉と呼ぶのは許容しよう。
型判断の意味はセマンティック・デカルト閉圏の射になる。特に集合圏では単なる写像。型コンテキストの意味は直積の形をした集合（方体状集合〈cube-shaped set〉）。型コンテキストや型判断で使われている名前〈ラベル | インデックス | キー〉は意味論に関係ない。
$`\Gamma \vdash M \equiv N :\sigma`$ という関数項の同値性判断（または等値性判断〈equality judgement〉）が出てくる。これは、高次圏の可逆2-射になる。集合圏の2-射は等式しかないので、同値性判断の意味は、写像の等式になる。
ベータ変換則〈beta rule〉とエータ変換則〈eta rule〉が、同値性の生成子になる。
命題項＝論理式の解釈〈意味論〉では、命題項の全体、またはその意味の集合は（ブール代数というより）ハイティング代数になると仮定する。
関手としての∀、∃と翻訳関手が自然変換になる条件がベック／シュバレー条件。
モデルが置換による作用と協調することがベック／シュバレー条件。
真偽対象〈truth object〉を持つようなデカルト閉圏から、ハイパードクトリンを作れる。真偽対象は命題値と論理順序〈logical order | implication order〉の内部圏。命題関数＝述語。命題項＝論理式。
ハイパードクトリンでは、真偽対象から述語空間〈述語集合〉が定義できる。
ハイパードクトリンに対する述語空間の構造はハイティング代数だが、ハイティング代数以外に選ぶことができる。
述語空間関手は反変で、選ばれた射に対して左右の随伴が存在してベック／シュバレー条件を満たす。
選ばれた射としては射影が多いが、選ばれた射のクラスは任意でよい。

様々なレベルのプログラミングが出来る。

型レベル・プログラミング：型リテラル、型変数、型コネクティブ〈型構成子記号〉から型項を組み立てるプログラミング。
データ・レベル・プログラミング：データ・リテラル〈ポイント・リテラル〉、データ変数〈通常の変数〉、データ・コネクティブ〈データ構成子記号〉からデータ項を組み立てるプログラミング。データ＝ポイント
関数レベル・プログラミング：関数リテラル、関数変数、関数コネクティブから関数項を組み立てるプログラミング。
置換レベル・プログラミング：置換リテラル、置換変数、置換コネクティブから置換項を組み立てるプログラミング。
命題レベル・プログラミング：命題リテラル、命題変数〈述語変数〉、命題コネクティブ〈論理コネクティブ〉から命題項〈論理式〉を組み立てるプログラミング。
導出レベル・プログラミング：導出リテラル〈公理〉、導出変数、導出コネクティブ〈リーズニング〉から導出項〈証明〉を組み立てるプログラミング。
リーズニング・レベル・プログラミング：リーズニング・リテラル、リーズニング変数、リーズニング・コネクティブからリーズニング項を組み立てるプログラミング。
構成手続きレベル・プログラミング：手続きリテラル、手続き変数、手続きコネクティブから構成手続き項を組み立てるプログラミング。

命題とデータは関数の特別なもの。置換は関数の集まり。

2022-07-21

型理論と論理のすり合わせ

半形式証明スクリプト論理用語法

まず、次は同義語扱いしたほうがいい。

変数の型宣言
型コンテキスト
0-指標
ポイント1-射だけの1-指標
構造体定義
レコード定義
テーブルスキーマ

例えば、

variable x, y : Real, c : Color

type-context {x:Real, y:Real, c:Color}

0-signature _ {
  0-mor x in Real
  0-mor y in Real
  0-mor c in Color
}

1-signature _  {
  1-mor x : 1 → Real in Set
  1-mor y : 1 → Real in Set
  1-mor c : 1 → Color in Set
}

struct ColoredPoint {
  Real x,
  Real y,
  Color c
}

record ColoredPoint {
  x: Real,
  y: Real y,
  c: Color
}

schema ColoredPoint {
  x : Real,
  x: Real,
  c: Color
}

ソート、ポイント1-射、変数型選言、法則からなる定義を伝統的指標と呼ぶ。

参考： U+21D2 ⇒ RIGHTWARDS DOUBLE ARROW, U+21D0 ⇐ LEFTWARDS DOUBLE ARROW

trad signature Monoid {
  sort U
  point m:[U ⇐ U×U]
  point e:U

  variable x, y, z : U
  law assoc :: m(m(x, y), z) = m(x, m(y, z))
  varible x : U
  law lunit :: m(e, x) = x
  law runit :: m(x, e) = x
}

伝統的指標は、無法則指標と型コンテキストと型コンテキスト上の論理式〈命題〉に分解できる。

無法則指標に対して、それから生成される型と関数の圏、型コンテキストと置換の圏が決まる。法則の命題は、ハイパードクトリンの生成系になる。

assoc-prop ∈ Prop[{x, y, z : U}]
lunit-prop, runit-prop ∈ Prop[{x : U}]

デカルト・ハイパードクトリンに対する演繹システムは、次の構文要素を持つ。

型項
関数項、複関数項、多関数項
型付き変数と型コンテキスト
置換〈代入〉射
命題項＝論理式
導出項＝マクロ導出
リーズニング項＝マクロリーズニング

Γ, Σ, Δ などは型コンテキストを表す。置換射〈substitution〉は S:Γ → Σ というプロファイルを持つ、これは導出とシーケントではない。

置換射は、反変的な翻訳関手〈translation functo〉 S^* = (-)[S] を誘導する。翻訳関手、翻訳関手の対象パート／射パートを置換〈代入〉と呼ぶことがある。

限量子は翻訳関手の左右の随伴パートナー関手として定義される。限量子は命題と導出の圏のあいだの関手である。

それと、$`\Gamma \mid \Theta \vdash \psi`$ 形式のシーケント（導出のプロファイル）において、

$`\Gamma`$ は型コンテキスト〈type context〉
$`\Theta`$ は命題コンテキスト〈proposition context〉
$`\psi`$ はターゲット命題〈target proposition〉

型コンテキストで宣言された自由変数しか命題内で使えない。

例：

$`\quad \{x:{\bf N}, y:{\bf N} \} \mid (\text{odd}(x), \text{odd}(y)) \vdash \text{even}(x + y)`$

2022-07-21

カリー／ハワード対応と相互関係

半形式証明スクリプト論理画像

型の圏（複圏、多圏もある）と命題の圏（複圏、多圏もある）との関係。カリー／ハワード／ランベック対応（むしろ、カリー／ハワード／ランベック・フレームワーク）があるので似てる。抽象化すれば同じになる。が、型コンテキストの圏の対象の上に命題の圏が乗って置換〈substitution〉と限量子で命題の圏が繋がる構造を持っている。一言で言えば、ハイパードクトリン。インスティチューションとしても定式化できる。

共通の用語や、異なる用語。

コンテキスト → 型コンテキスト、命題コンテキスト
コンテキストのラベル → 変数名／変数番号、命題名／命題番号
命題コンテキスト＝命題の宣言リスト（実体、データ型として）
命題コンテキスト＝仮定（役割として）
ターゲット → 関数のターゲット型〈戻り値型〉、導出のターゲット命題
ターゲット命題＝結論
シーケント〈プロファイル〉 → 型シーケント〈{複}?関数のプロファイル〉、命題シーケント〈導出プロファイル〉
スワップ射 → 型スワップ射、命題スワップ射
コピー射 → 型コピー射、命題コピー射
破棄射 → 型破棄射、命題破棄射
グラフティング → {複}?関数グラフティング、導出グラフティング
複結合 → {複}?関数複結合、導出複結合
ペアリング → 関数ペアリング、導出ペアリング
導出ペアリング＝連言導入
射影 → 型射影、命題射影
カリー化 → 関数カリー化、導出カリー化
関数カリー化＝ラムダ抽象
導出カリー化＝含意導入リーズニング
アンカリー化 → 関数アンカリー化、命題アンカリー化
関数アンカリー化＝関数適用
命題アンカリー化＝含意消去リーズニング
終対象 → 終型、終命題
終型＝ユニット型
終命題＝真命題
始対象 → 始型、始命題
始型＝空型
始命題＝偽命題
終型＝ユニット型
終命題＝真命題
終射 → 終関数、終導出
始射 → 始関数、始導出
恒等 → 恒等関数、恒等導出
General substitution
1. Substitution by Delete
2. Substitution by Copy
3. Substitution by Swap
4. Substitution by Function term

様々な規則

https://cs.au.dk/~birke/papers/categorical-logic-tutorial-notes.pdf の規則を列挙しておく。

型の圏の“規則”

IDENTITY 恒等単純関数がある／使える。
WEAKENING 破棄多関数をプレ多結合してよい。
CONTRACTION コピー多関数をプレ多結合してよい。
EXCHANGE スワップ多関数をプレ多結合してよい。
MULTI-COMPOSITION 多関数を多結合してよい。多関数項と多関数記号を組み合わる。
PAIRING 2つの複関数をペアリングして複関数を作ってよい。デカルト性。
PROJ-1 第一射影単純関数をポスト結合してよい。
PROJ-2 第ニ射影単純関数をポスト結合してよい。
ABS 複関数をカリー化してよい。
APP 複関数をアンカリー化してよい。エバル複関数と複結合してよい。
UNIT 終複関数がある／使える。

恒等単純関すと各種の結合が圏類似構造の公理だとして、次の基本構成の存在を要請している。

破棄多関数 Γ, σ → Γ
コピー多関数 Γ, σ → Γ , σ, σ
スワップ多関数 Γ, σ, σ' → Γ, σ', σ
第一射影単純関数 τ×σ → τ
第ニ射影単純関数 τ×σ → σ
終複関数 Γ → 1

射もモノイド積に相当するマージ規則を許せば、次のように単純化できる。

破棄多関数 σ → (,)
コピー多関数 σ → σ, σ
スワップ多関数 σ, σ' → σ', σ
第一射影単純関数 τ×σ → τ
第ニ射影単純関数 τ×σ → σ
終多関数 Γ → (,)

演繹の構造規則

IDENTITY 恒等単純導出がある／使える。
CUT 2つの複導出をグラフティングしてよい。
WEAK-PROP 破棄多導出ををプレ多結合してよい。
CONTR-PROP コピー多導出をプレ多結合してよい。
EXCH-PROP スワップ多導出をプレ多結合してよい。
WEAK-TYPE 破棄多関数で引き戻してよい。
CONTR-TYPE コピー多関数で引き戻してよい。
EXCH-TYPE スワップ多関数で引き戻してよい。
SUBSTITUTION 一般的な複関数で引き戻してよい。

プレ多結合してよい多導出は：

破棄多導出 Θ, ψ → Θ
コピー多導出 Θ, ψ → Θ, ψ, ψ
スワップ多導出 Θ, φ, ψ → Θ, ψ, φ

引き戻し〈置換 | 翻訳〉に使ってよい関数類は：

破棄多関数 Γ, σ → Γ
コピー多関数 Γ, σ → Γ , σ, σ
スワップ多関数 Γ, σ, σ' → Γ, σ', σ
一般的な複関数 Γ → σ （終複関数を含む）

論理の規則 so-called 自然演繹

TRUE 終複導出がある。
FALSE 始単純導出 ⊥ → ψ がある。仮定を水増しして Θ, ⊥ → ψ の形も使う。
AND-I 2つの導出の連言ペアリングをしてよい。直積ペアリングと同様。
AND-E1 第一射影単純導出がある。ポスト結合してよい。
AND-E21 第ニ射影単純導出がある。ポスト結合してよい。
OR-I1 第一入射単純導出がある。ポスト結合してよい。
OR-I2 第ニ入射単純導出がある。ポスト結合してよい。
OR-E 2つの導出の選言コペアリングをしてよい。直和コペアリングと同様。
IMP-I 複導出をカリー化してよい。
IMP-E 複導出をアンカリー化してよい。MP複導出と複結合してよい。
∀-I x:σ とういう変数を足して、破棄多関数 Γ, σ → Γ の置換の随伴が作れる。
∀-E 複関数 Γ → σ でインスタンス化できる。
∃-I 複関数 Γ → σ を証拠にして存在を主張できる。
∃-I x:σ とういう変数を足して、破棄多関数 Γ, σ → Γ の置換のもうひとつの随伴が作れる。

2022-07-21

MEDL、DIDLと背景理論と用語法

半形式証明スクリプト論理用語法

MEDL（Mathematical Entity Description Lang.）とDIDL（Drawing Instruction and Description Lang.）について。

DIDLはある程度は汎用の絵図記述言語。だが、直接的な目的は証明記述。「証明」は曖昧語なので、テクニカルタームとしては導出〈derivation〉を使う。「推論」もテクニカルタームとしては使わない。

「項」はテキスト記号表現〈テキスト・コンビネーション〉の意味で使う。項の種類は：

型項
関数項（定数項含む）
命題項＝論理式
導出項（＝証明項、使わない）

ここでの「定数項」はプロファイルが 1 → A の形の関数項のこと。ちなみに定数の意味は：

自由変数、束縛されてない変数
域が生成対象〈generator object〉である射
終対象／生成対象を経由する射
置換〈代入〉を許されない記号、リテラル、コネクティブなど

登場する圏類似構造

型の圏 ≒ 集合圏
型の複圏 ≒ 集合の複圏
型コンテキストの圏：対象は型コンテキストで、射は割り当て系〈system of assignment〉。射を置換〈substitution〉とは言わない。対象を型判断とは言わない。
命題の複圏：対象は命題で、複射は導出
命題の多圏：対象は命題で、多射は導出系〈system of derivations〉

型の圏、型の複圏は、型コンテキストの圏に埋め込める。型の多圏と型コンテキストの圏は、変数がある点で違う。

型コンテキストの圏の対象ごとに、そのコンテキスト上の命題の多圏が載る。インスティチューションまたはハイパードクトリン。型コンテキストの圏の射である割り当て系により置換または翻訳と呼ぶ引き戻し多関手が定義される。演繹システムの“規則”としては、引き戻し反変多関手（インスティチューションでは反変共変が逆になる）を SUBSTITUTION と呼ぶ。以下の“規則”はすべて SUBSTITUTION の特殊ケースとなる。

PROP-WEAKENING
PROP-COTRACTION
PROP-EXCHANGE
PROP-FUNCTION-TERM-SUBSTITUTION （狭義の SUBSTITUTION）

共通構造とカリー／ハワード／ランベック対応

型の圏と命題の圏は共通構造を持っている。

どちらもデカルト閉圏である。
したがって、モノイド積、単位終対象〈終対象対象〉、終射、カリー化／アンカリー化、ペアリング、射影〈破棄射〉、対角〈コピー射〉を持つ。
複圏または多圏のオペレータ（命題ではリーズニング）として次がある。IDENTITY, GRAFTING, MULTI-COMPOSITIO, WEAKENING, CONTRACTION, EXCHANGE。
型の圏がパイ型をサポートすると、∀限量子と同じ議論ができる。
型の圏も命題の圏もパイ構成を持つなら、λΠ-計算が出来る。圏の種別〈ドクトリン〉はCCCΠ〈Cartesian Closed Category with Π〉
SUBSTITUTION = TRANSLATION によって、インスティチューションまたはハイパードクトリン的な構造を導入できる。
命題の圏は、CCCなだけではなくて直和を持ち、デカルト閉半環圏になる。
命題の圏は、Π構造と双対なΣ構造も持つ。
型の圏と命題の圏は共通構造が多いので、同じ計算メカニズムが使える。
型の圏のなかに真偽値対象があれば、命題の圏を構成できる。この場合、命題を関数と思える。

用語法

型コンテキストを単にコンテキストということがある。
型コンテキストを型判断、または判断と呼ぶことがある。
割り当て系を判断と呼ぶことがある。
割り当て系を置換〈substitution〉と呼ぶことがある。
割り当て系の成分〈tuple component〉＝割り当てを判断と呼ぶことがある。
割り当て系の成分〈tuple component〉＝割り当てを置換と呼ぶことがある。
型コンテキストと指標が混同されることがある。型コンテキストを無法則指標とみなすことがある。
関数項による割り当てと、導出が混同されることがある。アビタである複圏が違う。
導出と導出のプロファイル〈シーケント〉が混同されることがある。
関数項を項と呼び、それ以外の項を項とは呼ばないことがある。
命題項は論理式と呼ぶ。
導出項を証明{項 | オブジェクト}と呼ぶことがある。
導出または導出項を推論と呼ぶことがある。特に基本導出{項}?を推論と呼ぶ傾向がある。
導出に作用するオペレータであるリーズニング、特に基本リーズニングを推論と呼ぶことがある。
リーズニングが含めたコンステレーション図のバエズ／ドーラン・ツリーを証明と呼ぶことがある。
ここでの置換は、項に作用する置換オペレータ〈置換リーズニング | 置換アクション | 置換コマンド〉である。
置換オペレータは関手なので、導出にも作用する。
置換オペレータ〈翻訳オペレータ〉＝置換関手〈翻訳関手〉の随伴により限量子〈量化子〉関手が定義される。
限量子関手の一部は限量子オペレータ。つまり、限量子リーズニング。