MP導出の図を向きを変える。
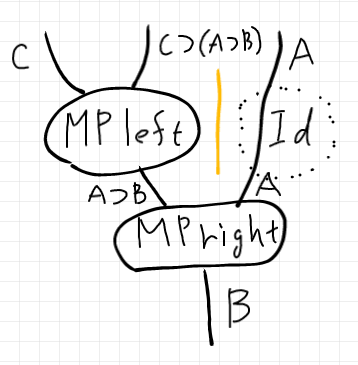
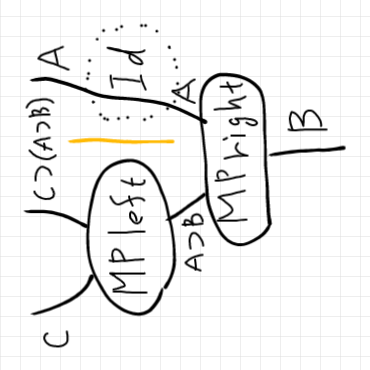
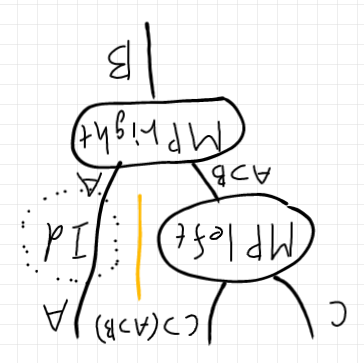
スタックとリストの関係と等式の証明
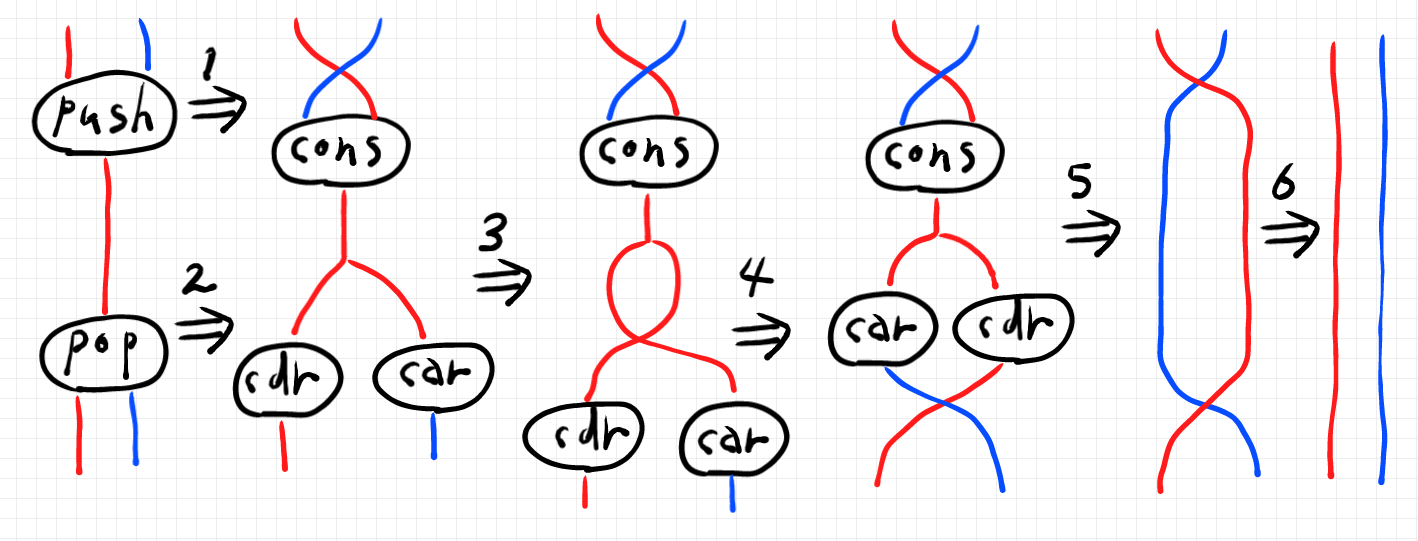
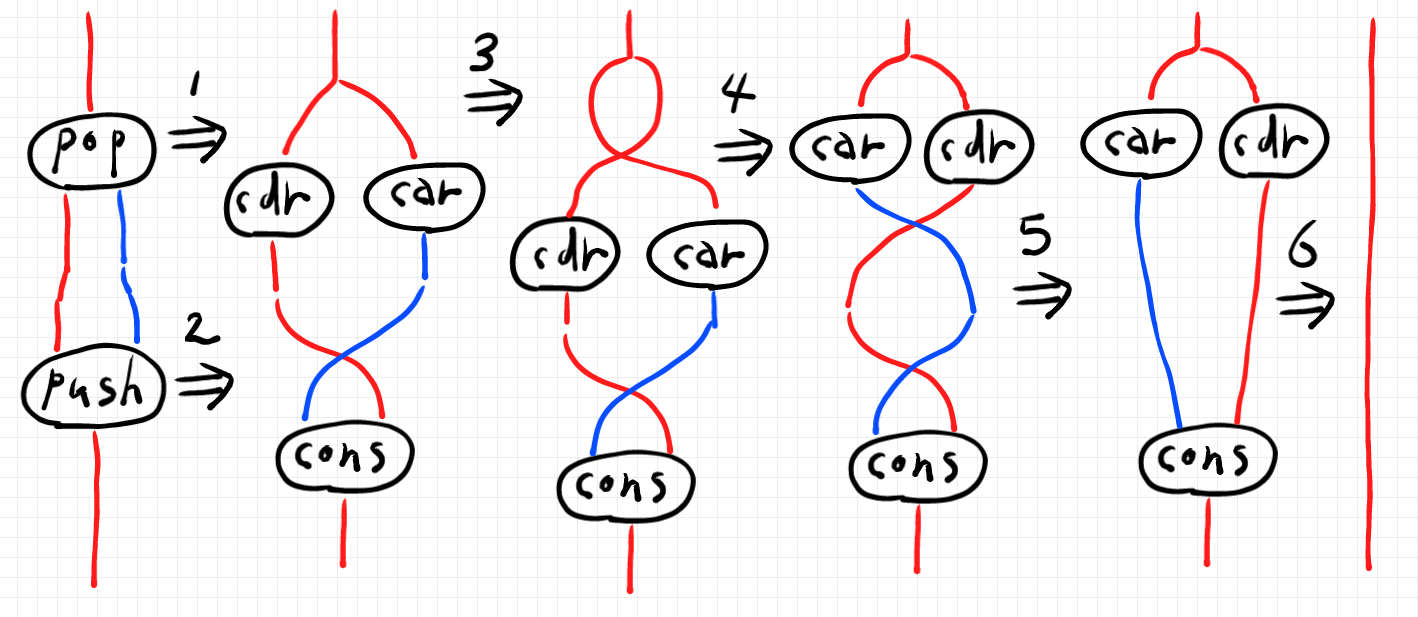
計算図
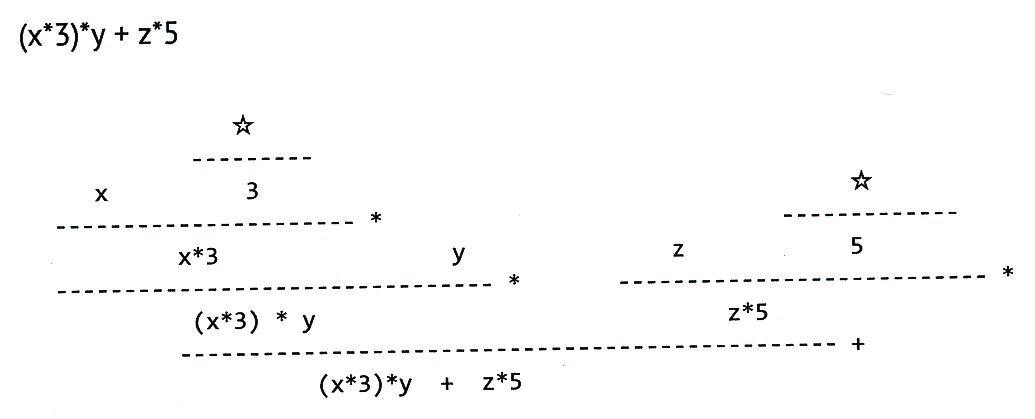
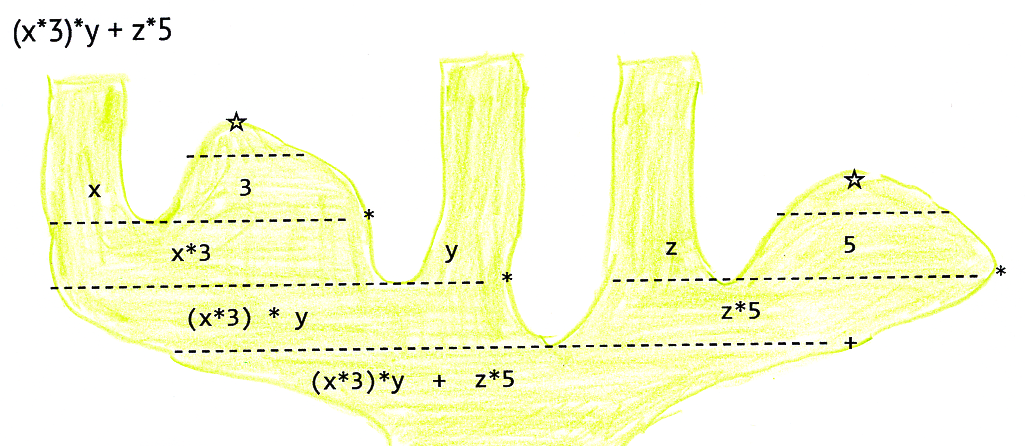
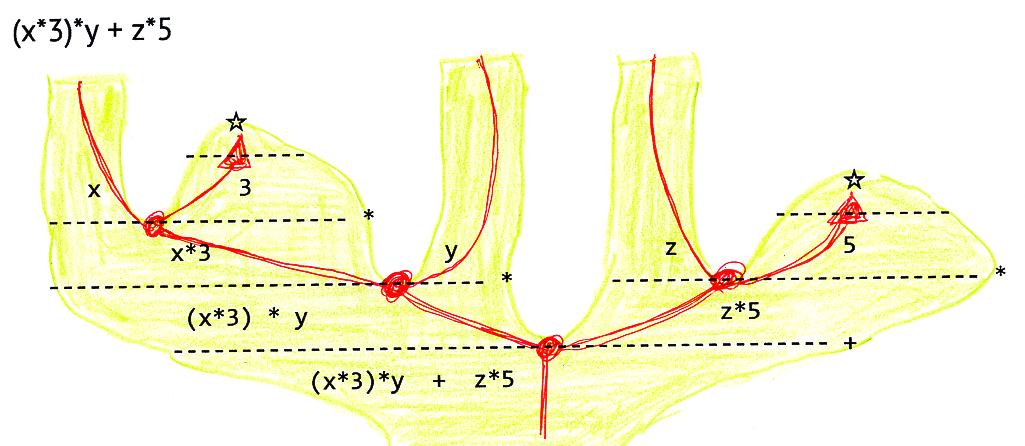
リーズニング図
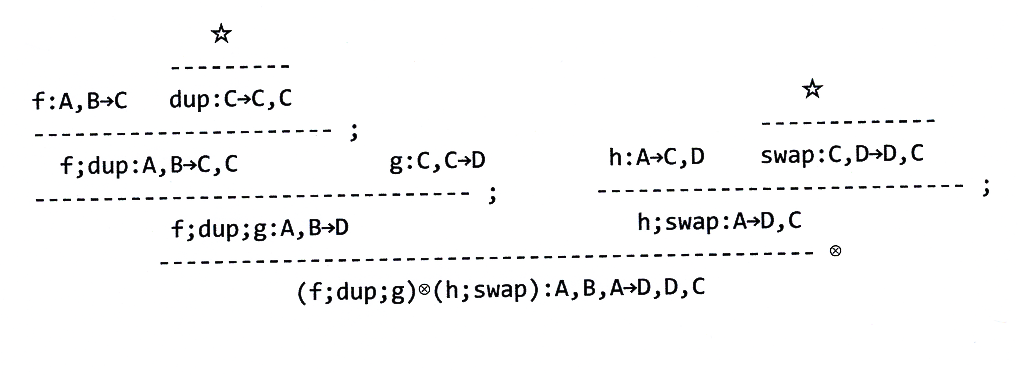
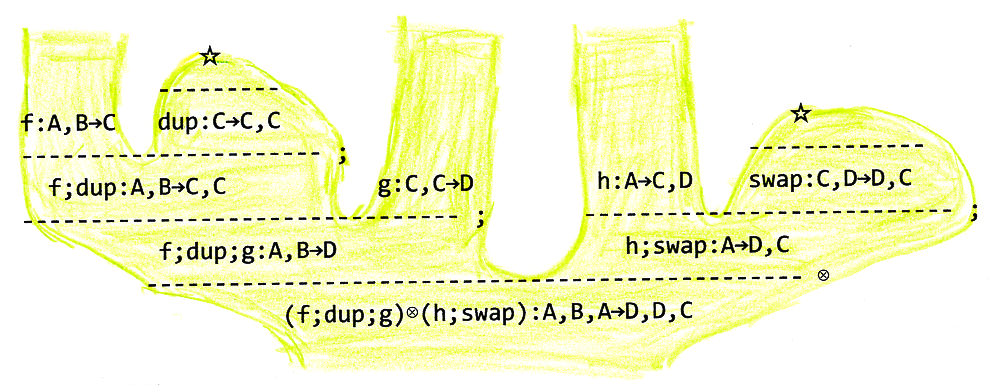
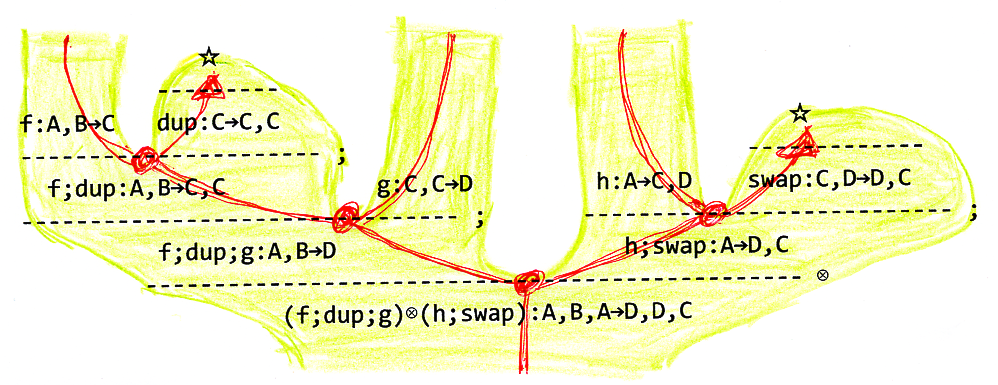
紙芝居方式リーズニング図
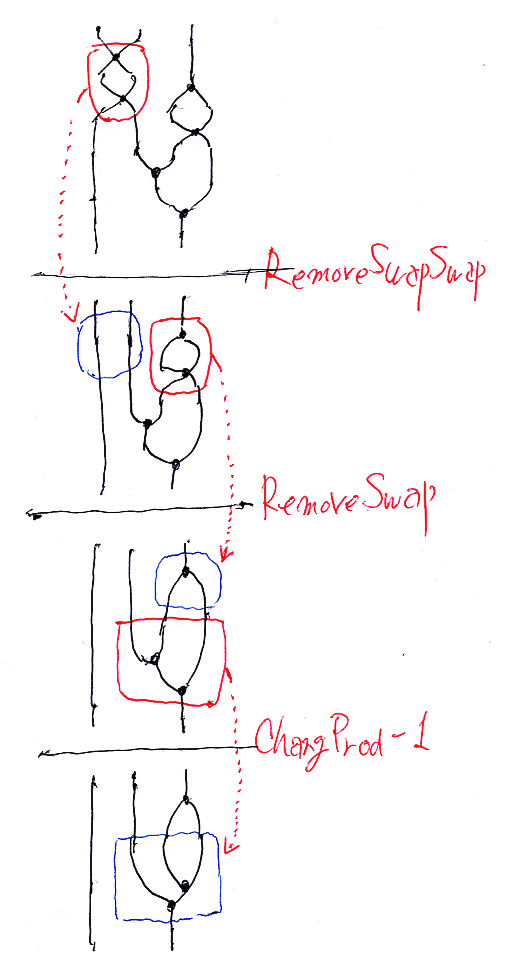
リーズニング図の同値変形
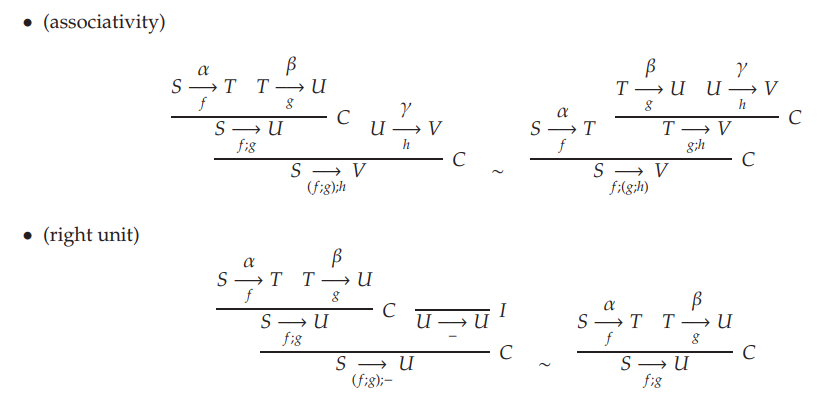
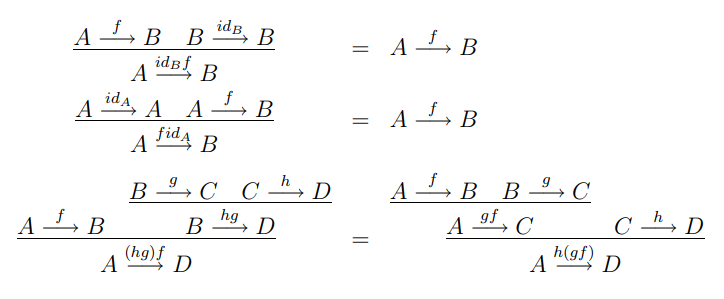
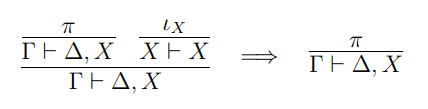
分岐合流紙芝居方式リーズニング図
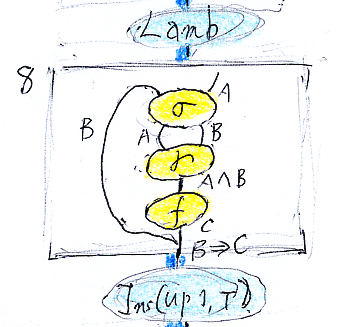
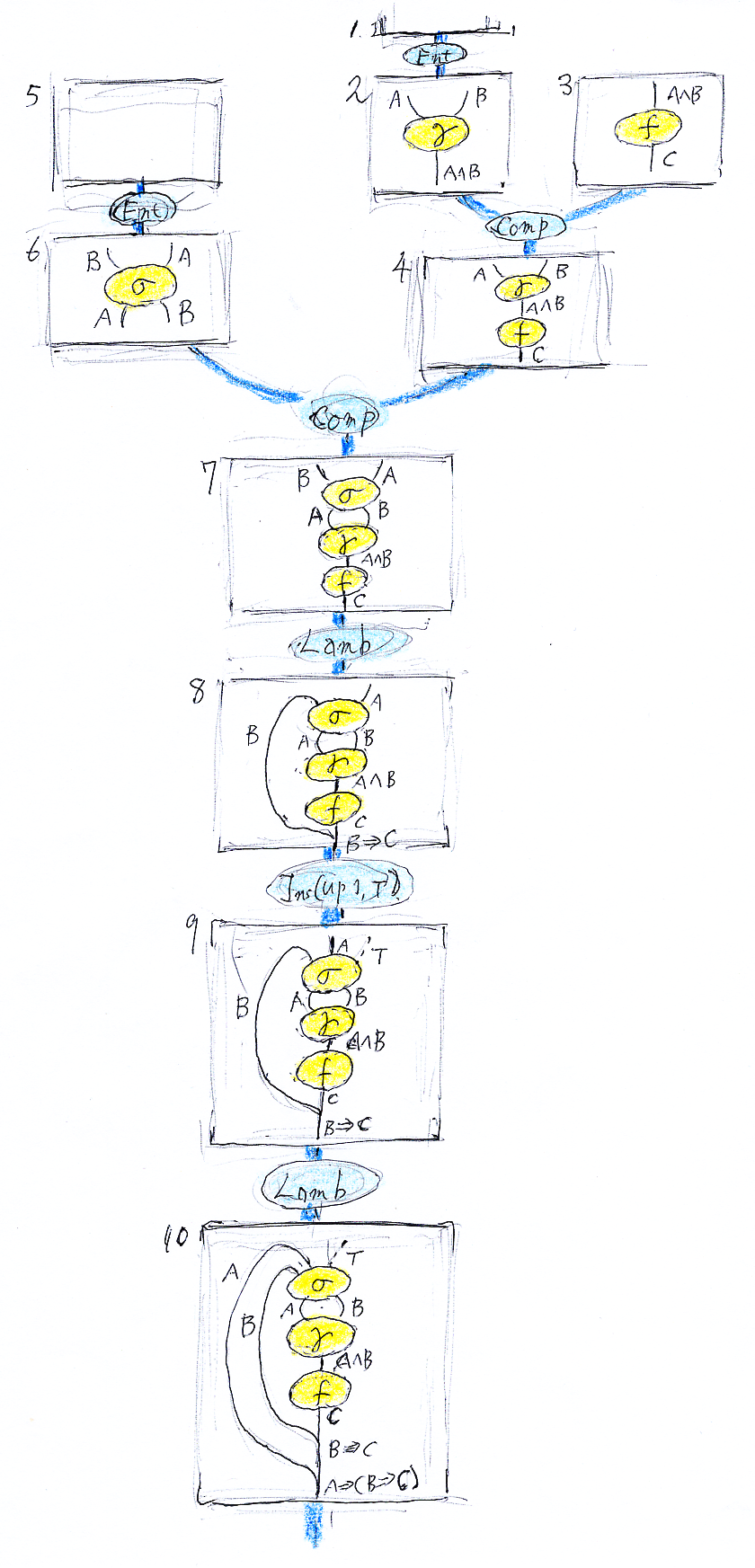
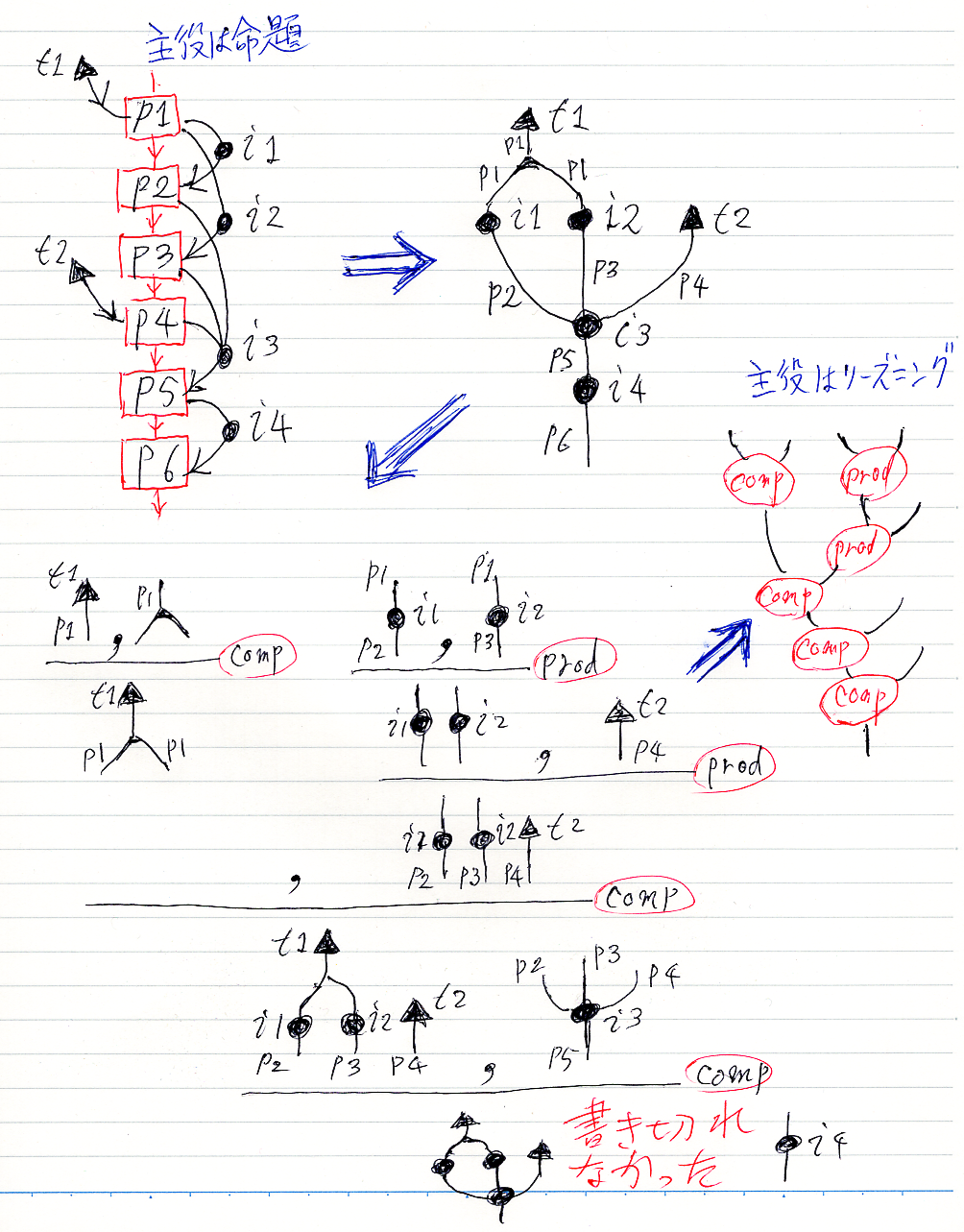
線形証明とグラフ証明図とツリー証明図
連言リストと宣言リスト、α, β は論域。
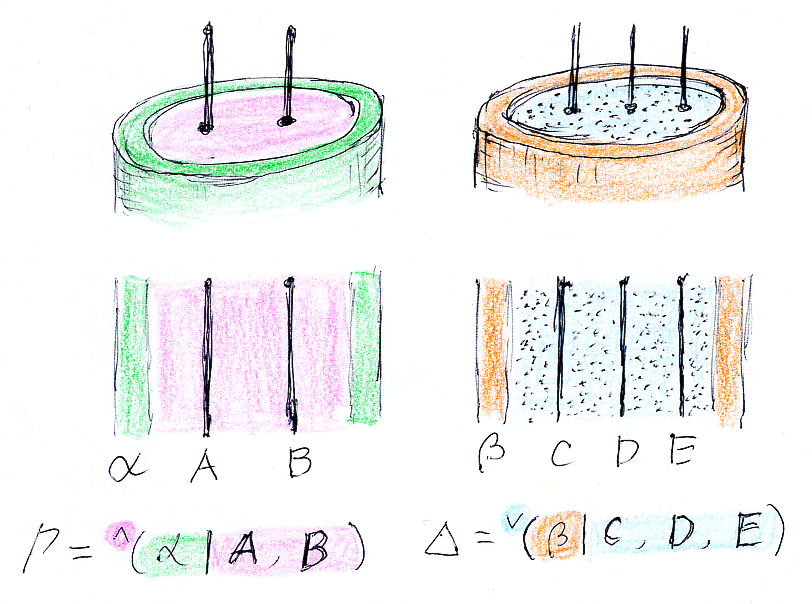
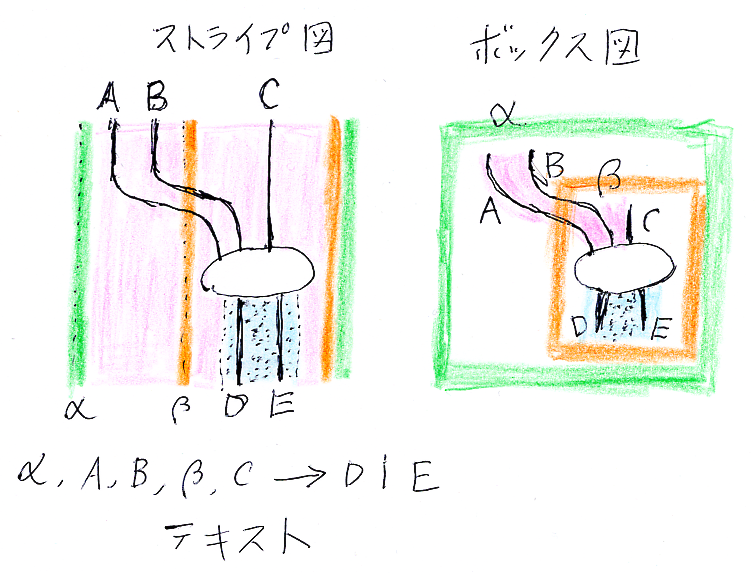
論域をストライプやボックスで表す。
定理と証明の構造
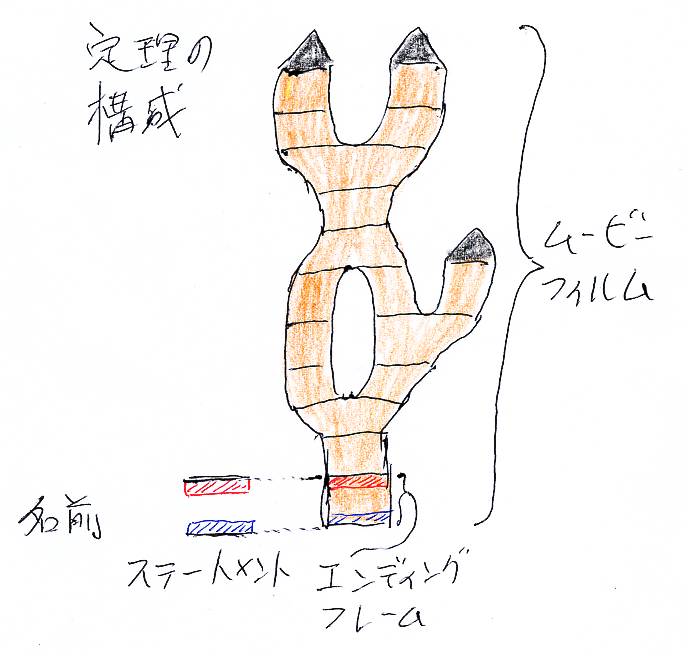
MP導出の図を向きを変える。



スタックとリストの関係と等式の証明


計算図
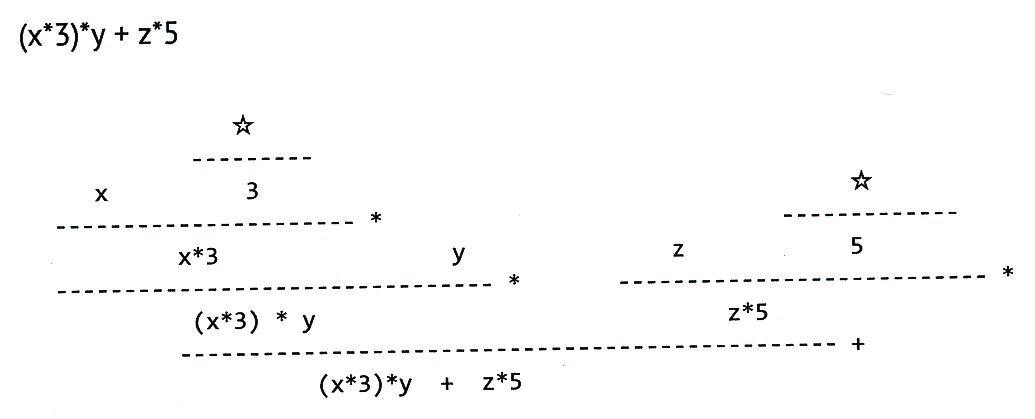


リーズニング図
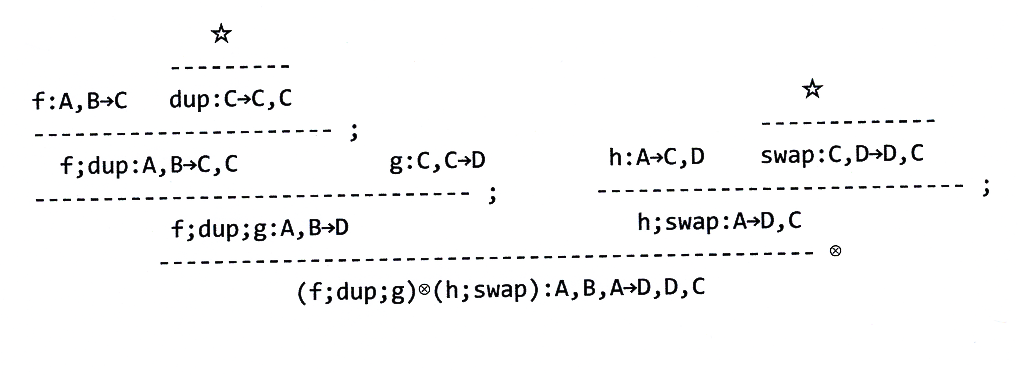


紙芝居方式リーズニング図

リーズニング図の同値変形
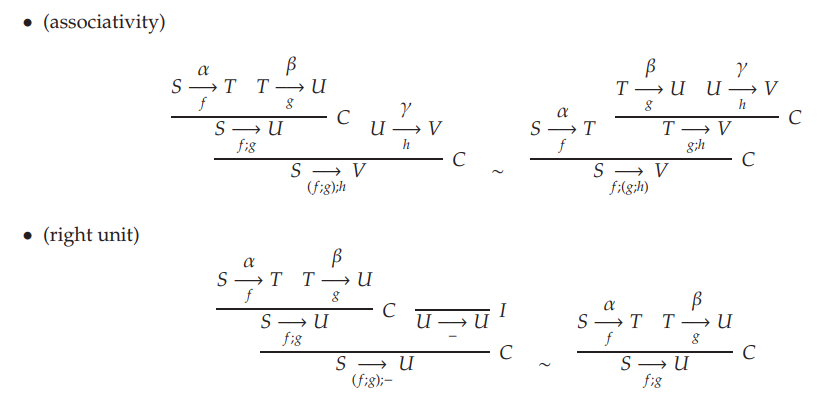
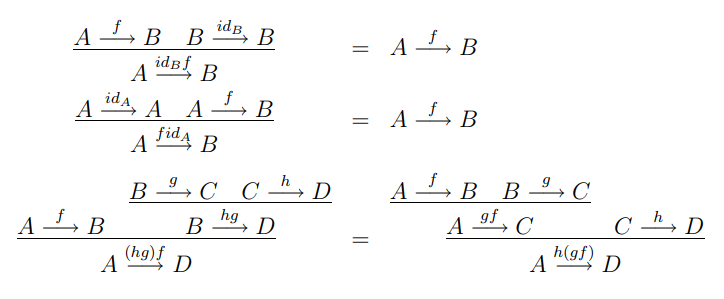
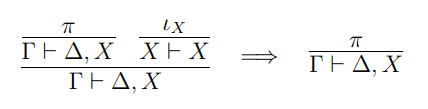
分岐合流紙芝居方式リーズニング図


線形証明とグラフ証明図とツリー証明図

連言リストと宣言リスト、α, β は論域。
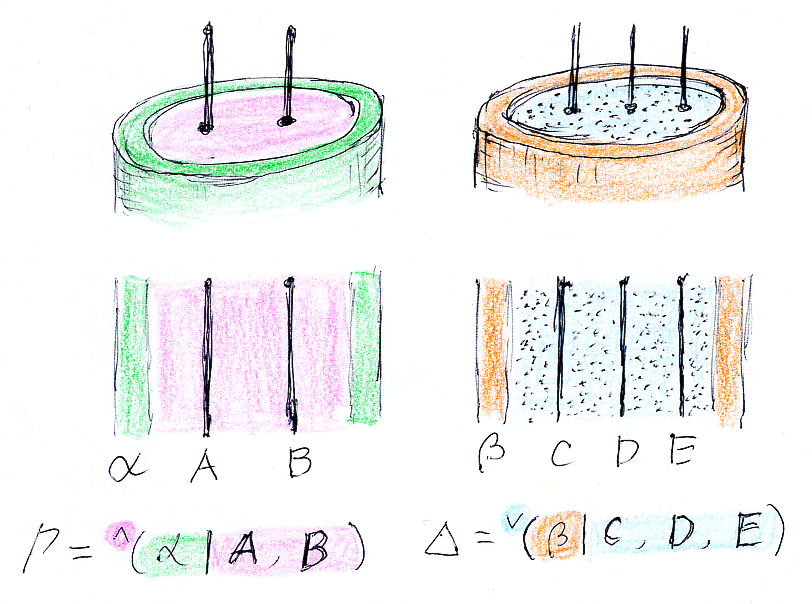
論域をストライプやボックスで表す。

定理と証明の構造

$`\newcommand{\derive}{ \vdash }%
\newcommand{\deduce}{ \mathop{\|\!-} }%
\newcommand{\afford}{ \mathrel{\|} }%
\newcommand{\Sign}[1]{ \mathscr{#1} }
\newcommand{\cat}[1]{ \mathcal{#1} }
\newcommand{\In}{ \text{ in } }
\newcommand{\ImpL}{ \Leftarrow }
\newcommand{\sto}{ \longrightarrow }
%`$次は同じ意味。
圏論的論理のチュートリアル - (新) 檜山正幸のキマイラ飼育記 メモ編 によれば、次も同じ意味。
少し違う点/同じ点は、
これは良いチュートリアルのように思えるが、「ゴッチャにした記述」が気になる。
typing rule として次の3つがある。
文法がらみは {syntax | syntactic{al}?} {formation | forming} rule のこと。構文範疇と型は違うが、しばしば混同される。p.4 の Figure 2 を typing rule と呼ぶのは酷すぎる。これは、論理式の文法生成規則。論理式が表すシングがPropと呼ばれるアビタに棲んでいる。
それに対して、p.3 Figure 1 は、デカル閉圏をアビタ(セマンティック背景圏)とする項〈式 | テキスト・コンビネーション〉の構成規則になっている。タイピング〈プロファイリング〉は構成に付随するオマケ的位置付け。セマンティクスを伴う項構成規則でプロファイルも計算可能な規則。
例によって、次は同義。
素材は:
オペレータは
当該チュートリアルのいい点は、シーケントの定義が明確な点だろう。シーケントは次の形に書かれる。
$`\quad \Gamma \mid \Xi \vdash \psi`$
Γは型コンテキストで、圏論的な指標になる。x:σ は x:1 → σ とみなすので、1-mor宣言がならぶことになる。型コンテキストとは限らない一般の指標をとってもいい。Γはセオリーを決めると言ってもいい。
Ξ は、論域が共通な命題〈論理式〉のリストで、
$`\quad \Xi = (\varphi_1, \cdots, \varphi_n)`$
したがって、シーケントの一部を抜き出すと、
$`\quad (\varphi_1, \cdots, \varphi_n) \vdash \psi`$
これは、命題の圏のプロファイル。シーケント全体としては、Γが定義する命題の圏のなかのプロファイルを意味する。そのプロファイルを持つ射 F が導出(通常「証明」とも呼ばれる)。X は論域。
$`\quad F : (\varphi_1, \cdots, \varphi_n) \to \psi \text{ on } X \text{ in }\mathrm{Prop}[\Gamma]`$
「シーケントが証明できる」とは、そのシーケント=プロファイルを持つ導出が構成可能であること。
p.40に自然演繹の規則が書いてある。これをチャンと圏論的・絵算的に書き換えて、最終的にDIDLで書く。
https://cs.au.dk/~birke/papers/categorical-logic-tutorial-notes.pdf の P.3 の11個の規則
使う文は以下。
確認と取得
新規導入
操作
象形文字 I
from wire-palette we get σ we use make-id we assert σ → σ
象形文字 !
we possess M:Γ → τ we use pre-compose id[Γ], Delete[σ] we assert Γ, σ → τ
象形文字 Δ
we possess M:Γ, σ, σ → τ we use pre-compose id[Γ], Copy[σ] we assert Γ, σ → τ
象形文字 X
we possess M:Γ, σ, σ' → τ we use pre-compose id[Γ], Swap[σ, σ'] we assert Γ, σ', σ → τ
記号 -(-, ..., -)
from node-palette we assert F:τ_1, ‥‥, τ_n → τ' we possess F:τ_1, ‥‥, τ_n → τ' we possess M_1:Γ → τ_1 ‥‥ ‥‥ we possess M_n:Γ → τ_n we use left multi-composition we assert Γ → τ' due-to F(M_1, ..., M_n)
記号 < -, - >
we possess M:Γ → τ we possess N:Γ → σ we use pairing[Γ, τ, σ] we aasert Γ → τ×σ du-to <M, N>
記号 π^1
we possess M:Γ → τ×σ we use post-compose proj-1[τ, σ] we assert Γ → τ
記号 π^2
we possess M:Γ → τ×σ we use post-compose proj-2[τ, σ] we assert Γ → σ
仮想ベンディング象形文字 ∩
we possess M:Γ, σ → τ we use curry[Γ, σ, τ] we assert Γ → [σ, τ]
仮想ベンディング象形文字 ∪
we possess M:Γ → [τ, σ] we possess N:Γ → τ we use left uncurry[Γ, σ, τ] we assert Γ → σ
象形文字 !
we have Γ we use make-terminal[Γ] we assert Γ → 1
面積問題への対策(あるいは無策) (A21) - (保存用) 檜山正幸のキマイラ飼育記 メモ編 2019-01-08
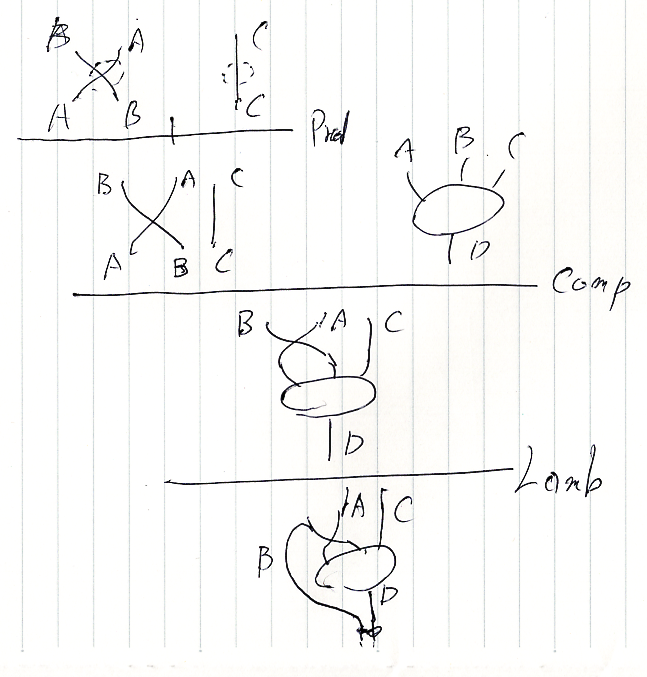
意味不明な言葉達 - (保存用) 檜山正幸のキマイラ飼育記 メモ編 2018-11-15

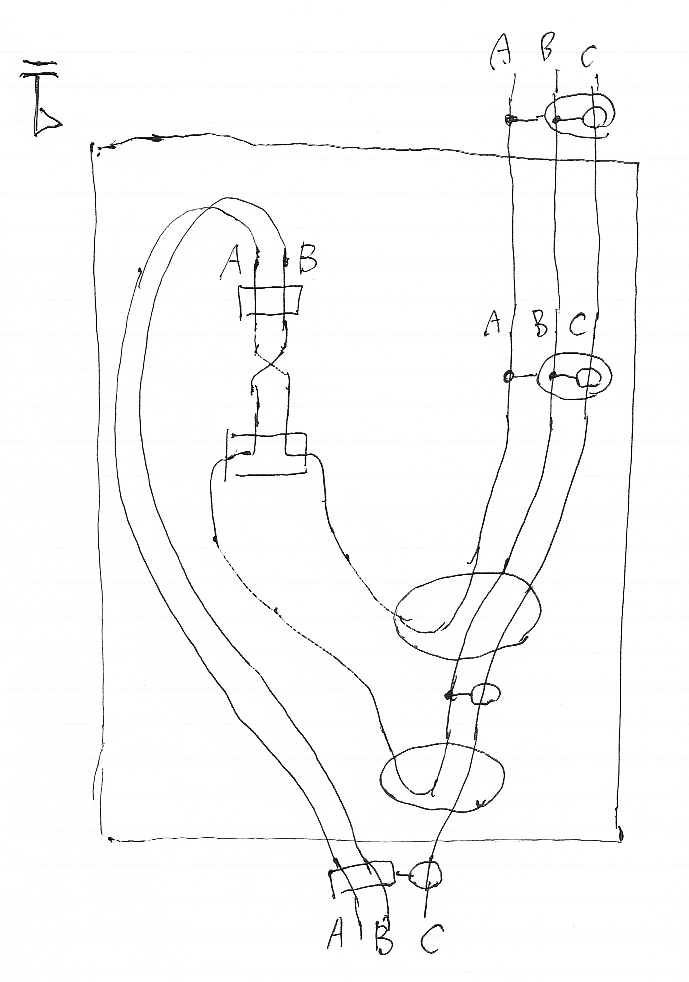
お絵描き証明の例 - (保存用) 檜山正幸のキマイラ飼育記 メモ編 2016-02-24
$`\varphi : A\Rightarrow(B\Rightarrow C) \longrightarrow (A\land B)\Rightarrow C`$
関数なら:
$`f : A\Rightarrow(B\Rightarrow C) \rightarrow (A\times B)\Rightarrow C`$
証明オブジェクトとしてのラムダ項 - (保存用) 檜山正幸のキマイラ飼育記 メモ編 2017-08-25

CoqでもLeanでもPropを使うが、Prepの正体は何でもよくて、デカルト閉半環圏(の対象集合)であればよい。自然数上に定義された述語 p は
だが、その実体が次のいずれでも、さらに他の何かでもいい。
$`\quad p:{\bf N} \to {\bf B} \text{ in }{\bf Set}`$
$`\quad p:{\bf N} \to |{\bf Set}| \text{ in }{\bf SET}`$
ストリング図の描画指令〈instruction〉と記述〈description〉のための言語
目的は違うが名前が似ているもの:
絵の構成素は:
書き換え操作をグループに適用するときは、Using operatin を使う。
描画指令文/操作指令文と確認文とグルーピングブロックの組み合わで図を記述する。
構文は:
law 2-ラベル :: 閉じた論理式
または
variable 変数の型宣言 law 2-ラベル :: 自由変数を含む論理式
法則の圏論的実体〈シング〉は2-射なので、法則名は2-ラベルとする。
事例:
signature LawlessMonoid within Set {
sort U
operation e: 1 → U
operation m: U×U → U
}法則を付け加える。
signature Monoid within Set {
sort U
operation e: 1 → U
operation m: U×U → U
law assoc :: ∀x, y, z∈U. m(m(x, y), z) = m(x, m(y, z))
law lunit :: ∀x∈U. m(e, x) = x
law runit :: ∀x∈U. m(x, e) = x
}または
signature Monoid within Set {
sort U
operation e: 1 → U
operation m: U×U → U
variable x, y, z∈U
law assoc :: m(m(x, y), z) = m(x, m(y, z))
law lunit :: m(e, x) = x
law runit :: m(x, e) = x
}
信頼できる談話環境〈trustable discourse environment〉とは、そのなかでの発話行為、または記載(何かが書いてある)がそのまま事実と解釈してよい環境。
一番外側の記述は、信頼できる談話環境のなかにあると考える。そうでないと、「‥‥はほんとうか?」の永久後退が生じて、判断〈judgement〉ができない。信頼できる談話環境では、自動的に判断が出来る。
ある発話や記載が信頼できないときは、信頼できる談話環境内でその発話・記載をサブジェクトにした議論をする。
導出とシーケントを混同する理由 - (新) 檜山正幸のキマイラ飼育記 メモ編 に関連して。
信頼できる目録があるとする。目録に登録されていることが、存在を保証するならば、
演繹システムのシステム指標/ライブラリ指標は、信頼できる目録だから、指標に登録されていると、それはセマンティック背景圏の対象・射・オペレータ・2-射などの存在命題になる。存在命題(インデックス付き存在命題)に対するスコーレム関数は、インデックス付き族となる。
インデックス付き族を“規則”と呼んでいるのだろう。インデックスを具体化することが規則の具体化。規則の具体化は、全称命題の具体化ではあるが、メタ全称命題(インデックス付き存在命題は全称命題)の具体化に対応する。
演繹システムにおいては、次が同じ効果を持つ。
登録が、メタなインデックス付き存在命題を主張することと同じであることが見過ごされやすい。また、スコーレム関数があれば十分だが、構成的・具体的に与えられることが多い。
既存導出を組み合わせて新しい導出作ることにより証明を行う。このとき、実際の導出が何であるかは問題にならない。なので、シーケント〈導出のプロファイル〉を書くだけで導出を書いたことになる。これより、導出とシーケントが混同、あるいは同一視される。
A∧B → A はプロファイルだが、次の命題を考える。
これが真だとして、スコーレム関数 ψ を考える。
これは ψ:Obj(C)×Obj(C) → Mor(C) という関数を定義する。射のインデックス付き族になる。
今は 射=導出 だから、導出のインデックス付き族になり、それを推論規則と呼ぶ。時系列で書くと:
ここで注意すべきは、スコーレム関数さえあればよいこと。ψがほんとの射影である必要はない。ψを具体的に与えるとき典型的・簡単なのは射影だが、“規則”の実体が射影である必要性がない。
ここにギャップがある。仕組み上は射影である必要がないが、たいていはスコーレム関数の具体的な実現として射影を想定している。
次の概念のあいだの相互関係をよく理解すべきだ。
$`\newcommand{\derive}{ \vdash }%
\newcommand{\deduce}{ \mathop{\|\!-} }%
\newcommand{\afford}{ \mathrel{\|} }%
\newcommand{\Sign}[1]{ \mathscr{#1} }
\newcommand{\cat}[1]{ \mathcal{#1} }
\newcommand{\In}{ \text{ in } }
\newcommand{\ImpL}{ \Leftarrow }
\newcommand{\sto}{ \longrightarrow }
%`$
対応があまりピッタリではないが。
| 演繹システム | 類似の既存用語 |
|---|---|
| sys-prop | 論理定数 |
| sys-deriv | 論理公理 |
| sys-reas | 推論規則 |
| sys-equiv | 論理法則 |
| user-prop | ? |
| user-deriv | 分野公理 |
| user-reas | 分野推論規則 |
| user-equiv | 分野論理法則 |
システムを次のように置く。
$`\quad \mathscr{D} = (\mathscr{D}_\mathrm{prop}, \mathscr{D}_\mathrm{deriv}, \mathscr{D}_\mathrm{reas}, \mathscr{D}_\mathrm{equiv})`$
ライブラリは:
$`\quad \mathscr{L} = (\mathscr{L}_\mathrm{prop}, \mathscr{L}_\mathrm{deriv}, \mathscr{L}_\mathrm{reas}, \mathscr{L}_\mathrm{equiv})`$
演繹可能性は:
$`\quad \mathscr{L} \deduce_\mathscr{D} \Gamma \sto B`$
演繹定理から:
$`\quad \mathscr{L}, \hat{\Gamma} \deduce_\mathscr{D} (,) \sto B`$
あるいは、
$`\quad \mathscr{L}, \hat{\Gamma} \deduce_\mathscr{D} (\vdash B)`$
順不同。
TypeScriptと比較する。
| TypeScript | Tenjin MEDL | 備考 |
|---|---|---|
| スクリプト | ノートパッド | 使い捨て |
| モジュール | アーティクル | .medl.md ファイル |
| パッケージ | パッケージ | 同じNPM構造 |
| 名前空間 | デビジョン | division |
| インターフェイス | 指標 | signature |
| 総称クラス | 構成手続き | procedure |
| 抽象クラス | デビジョン | division |
| .d.ts ファイル | ライブラリ指標 | .medls.json ファイル |
アーティクルの雛形
---
file: foo.medl.md
tags: foo
title: foo
---
article foo
declare A in Set
declare B in Set
define foo1 : A → B in Set := ...
divison bar {
declare ...
}
devision baz {
}
signature zot {
}