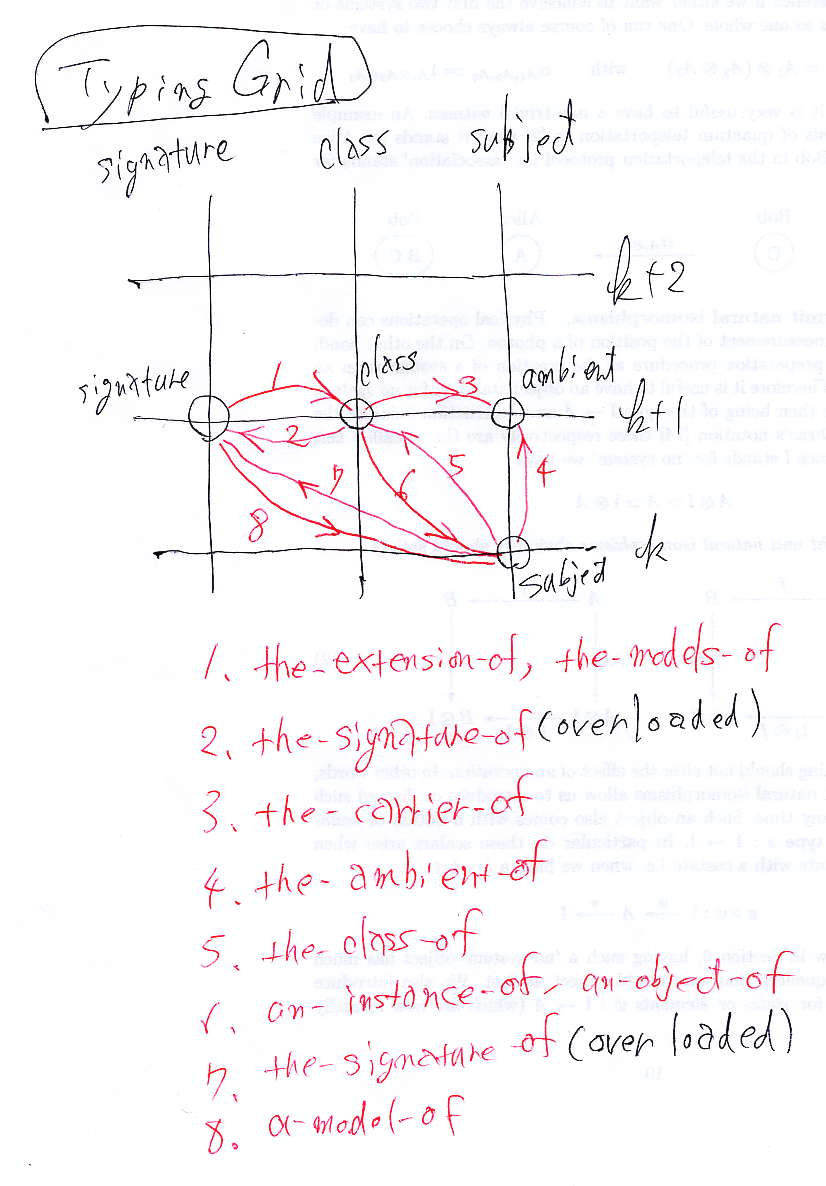
横と縦があるので、
- 縦方向の列=ピア〈pier〉(peerではない!)
- 横方向=フロア
- フロアの数=ストーリー
次のように呼ぶのが良さそう。∈0 は「対象として所属する」。
- 指標Σ ∈0 リテラチャーL
- ターゲット圏C ∈0 アンビエントA
- 指標とターゲット圏から決まるクラスは Mod(Σ, C) ∈0 アンビエントA
- 指標Σのメタ指標Σ'があり、アンビエントAは、メタ指標Σ'のクラス(メタクラス)のインスタンスである。このとき、メタクラスのターゲット(2-圏になる)やアンビエント(メタアンビエント)は明示されないことが多い。
今までの用語法の欠点は:
- 指標とリテラチャー(指標圏)の区別が付きにくい。
- ターゲット圏とアンビエントの区別がとても付きにくい。どちらもアンビエントと呼んでいた気がする。また、アンビエントは2-圏(圏の圏)だし、ターゲットは圏である事実も忘れがち。
ここで、 クラスは型クラスの意味であり、指標とターゲットに対して相対的に定義される。次の欠点は残っている。
- クラスが型クラスなのか型インスタンスなのか分からない。
「メタ」の用法は、
- 指標はメタ指標により支配されている。スーパー指標〈上位指標 | 基底指標 | 優指標〉とサブ指標〈下位指標 | 派生指標 | 劣指標〉の関係と、指標/メタ指標の関係は別物。
- クラスはモデル構成関手の“値”のことで、アンビエントのインスタンス〈対象〉。したがって、メタクラスはアンビエントと言えるが、あまり「メタ」にふさわしくない。
- メタアンビエントを、アンビエントをインスタンスとする圏だとすると、それは一階上のフロアのクラスになる。
今述べた「メタ」の用法はけっこうグチャグチャ。
- 指標 → メタ指標 : 階数が一階上がる。指標はメタ指標(空かも知れない)なしでは存在し得ない。必然性がある。
- クラス → メタクラス : 単にモデル構成関手の具体的値と余域の関係。必然性がないし、用法としてもズレている。
- アンビエント → メタアンビエント : アンビエントとメタアンビエントのあいだにはインスタンス所属関係がある。しかし、メタアンビエントはアンビエントではなくて一階上のクラスになる。
メタ指標以外は「メタ」使わんほうが無難。
Xがインスタンスとして所属するn-圏を「Xのn-クラス」と呼ぶことにすると、n階のサブジェクトは、(n+1)階のクラスに所属する。これは、タイピング・グリッドで斜め線になる。n-階にいるアンビエントはn-圏ではあるが、(n+1)構造を持つ圏からトランケーションしている。トランケーションにより得られるn-圏は打ち切りn-圏と呼ぶ。アンビエントは、n圏を対象とする打ち切りn-圏である。打ち切りという犠牲の代償として内部ホム構造を手に入れている。
打ち切りn-圏であるn-階のアンビエントは、(n+1)階のクラスである(n+1)-圏のインスタンスになる。
注意すべき点のまとめ: