全称限量子とタプル - (新) 檜山正幸のキマイラ飼育記 メモ編:
もっと考えないと。
最初に、 連言ボックス、選言ボックス、全称ボックス、存在ボックス - (新) 檜山正幸のキマイラ飼育記 メモ編 と 選言ボックスと二面ノード - (新) 檜山正幸のキマイラ飼育記 メモ編 から絵だけ再掲する。
連言ボックス、選言ボックス、全称ボックス、存在ボックス - (新) 檜山正幸のキマイラ飼育記 メモ編
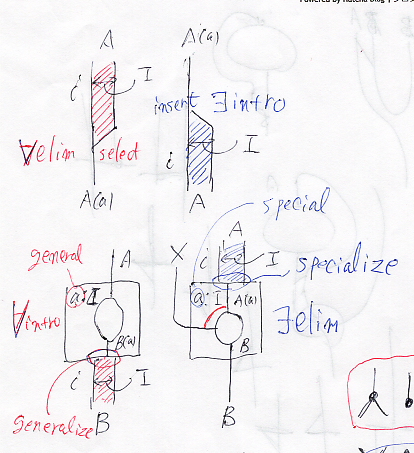
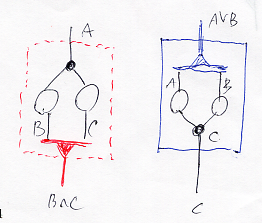
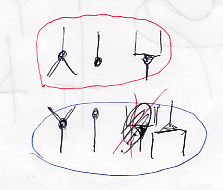
選言ボックスと二面ノード - (新) 檜山正幸のキマイラ飼育記 メモ編
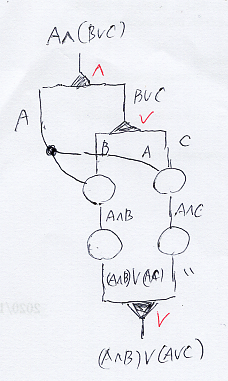
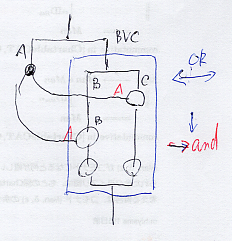
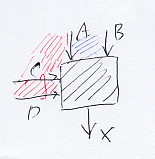
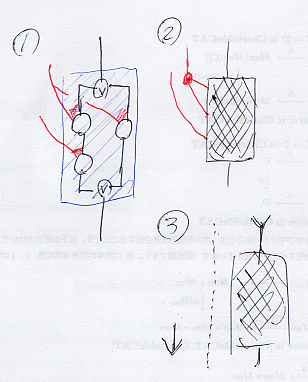
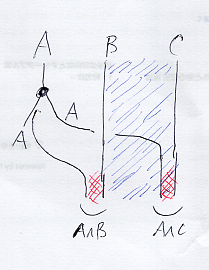
古典論理の発想では次の関係がある。
$`
\xymatrix {
{\rm finite} \ar@{.}[r]
&*++{\land} \ar@{<->}[rr]^-{\rm De\: Morgan\: dual} \ar[d]_-{\rm parameterize}
&
&*++{\lor} \ar[d]^-{\rm parameterize}
\\
{\rm allows\: infinite} \ar@{.}[r]
&*++{\forall} \ar@{<->}[rr]_-{\rm De\: Morgan\: dual}
&
&*++{\exists}
}
`$
古典論理の特徴は、排中律、二重否定、背理法だが、対偶関手〈contraposition functor〉に二重否定から背理法は出る。
- 対偶関手 $`(\mbox{-})^\dagger : {\bf NDed}(A, B) \to {\bf NDed}(\lnot B, \lnot A)`$
反変関手である対偶関手の対象部分が否定になる。否定が厳密対合であることが二重否定の法則。
古典論理の全称限量子は、上記のド・モルガン四角形〈De Morgan square〉のなかで位置付けるのが適切だが、依存型理論を使う方法だと、全称限量子は次の位置付けだと思う。
$`
\xymatrix {
{\rm independent} \ar@{.}[r]
&*++{\to} \ar[d]_-{\rm dependency}
\\
{\rm dependent} \ar@{.}[r]
&*++{\forall}
}
`$
それを以下で見る。
まず集合ベースで
X∋x → P(x) 型ファミリー ------------------- パイ型形成子 Πx∈X.P(x) 型 X∋x → f(x)∈P(x) 値ファミリー along 型ファミリーP ------------------- 依存関数データ=ヘテロタプル構成子 〈f(x)〉x∈X:Πx∈X.P(x) 依存関数データ
特殊な形として、
X∋x → A 定数型ファミリー ------------------- パイ型形成子 Πx∈X.A = [X, A] 型 X∋x → f(x)∈A 値ファミリー along 定数型ファミリーA ------------------- 関数データ=一様タプル構成子 〈f(x)〉x∈X:[X,A] 関数データ
記法を変える。
x:X ⇒ P(x) 型ファミリー ------------------- パイ型形成子 Πx∈X.P(x) 型 x:X ⇒ f(x):P(x) 値ファミリー along 型ファミリーP ------------------- 依存ラムダ抽象 Λx:X.f(x) : Πx:X.P(x) 依存関数データ=ヘテロタプル
x:X ⇒ A 定数型ファミリー ------------------- パイ型形成子 Πx:X.A = X→A 型 x:X ⇒ f(x):A 値ファミリー along 定数型ファミリーA ------------------- ラムダ抽象 λx:X.f(x): X→A 関数データ=一様タプル
さらに別記法。
x:X |- P(x) :Type ------------------- パイ型形成子 Πx∈X.P(x) :Type x:X |- f(x):P(x) ------------------- 依存ラムダ抽象 Λx:X.f(x) : Πx:X.P(x)
x:X |- A :Type ------------------- パイ型形成子 Πx:X.A = X→A :Type x:X |- f(x):A ------------------- ラムダ抽象 λx:X.f(x): X→A
まだ続く。