連言ボックス、選言ボックス、全称ボックス、存在ボックス - (新) 檜山正幸のキマイラ飼育記 メモ編 の続き。
モヤモヤを晴らすためにすること。
- ラムダ項の圏論的位置付けをハッキリさせる。
- 単なる圏ではなくて復圏〈オペラッド〉を使う。
- デカルト閉復圏=デカルト閉オペラッド=閉クローン を使う。
- デカルト閉圏Cから MultiC を作る。
- ケーブルとワイヤーを徹底的に区別する。
- ケーブルへの型ラベルと名前ラベルを徹底的に区別する。名前ラベルは番号で置き換え可能。
- ケーブルを連言ケーブル〈直積ケーブル〉、選言ケーブル〈直和ケーブル〉、含意ケーブル〈指数ケーブル〉に分ける。
- 外部カリー化〈抽象〉と内部カリー化〈型の変換〉を区別する。外部カリー化は圏論的オペレータ、内部カリー化はケーブル・リアレンジ・ボックスで表す。
- ケーブルの幅が無限である全称ケーブルと存在ケーブルも考える。
- ケーブルの幅が無限である含意〈指数〉ケーブルが問題・疑問・課題だ。
- 幅無限の含意〈指数〉ケーブルが依存関数型だと思う。
- 上下左右を厳しく区別する。
まず、復圏の復射とラムダ射の関係。復射とラムダ射は別世界にいるとする。

ラムダ射は、入力無しで、右から左に番号が付き、左端だけは番号が付かない。左端ではないワイヤーをラムダワイヤー〈lambda wire〉と呼ぶ。これは、ラムダ関数項のラムダ引数リストのラムダ引数項目に相当する。ラムダワイヤーは最も重要な概念。
ラムダワイヤーは出力側で便宜上反対方向を持つと考える。ラムダワイヤーではない(上からの)入力ワイヤーがあってもよさそうだ。
復圏の復射をラムダ射に変換するのが関数抽象=外部カリー化。
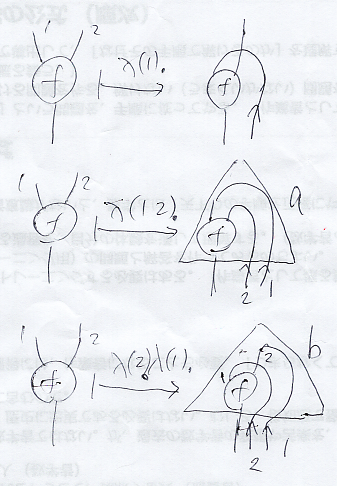
関数抽象=外部カリー化は、上の入力ワイヤーの番号(左から右)で識別できるワイヤーベンディング・オペレータ。一番目の外部カリー化だと、入力ワイヤーが残るので、入力ワイヤーを許すラムダ射(大きなラムダ式に相当)も許すほうがよさそう。
うまく定義すれば、復射とラムダ射を同じ世界で考えることが出来るかも知れない。
次の図は、ワイヤー組み替え〈wire {altering | rearrange | recombination}〉の事例。まだちゃんと分かってない。
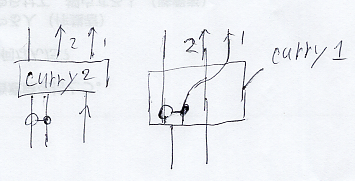
対称〈スワップ | 交換 | 換〉と内部カリー化/内部反カリー化により、ケーブルの構造を変えること。ラムダ射の世界におけるスパイダリングがワイヤー組み替え。
ラムダ射の世界では、ラムダ抽象=外部カリー化 λ(i) (i は番号列)と左引数評価 ▷i と右引数評価 ◁i がある。ラムダ射の世界は確率的アレンジメントの世界と類似している。二部アレンジメントの二部構造=分割が固定されている。一般的には、アレンジメント代数と言えそうだ。
復射の世界=復圏では、オペラッド結合 ;i, i がある。フルカリー化/フル反カリー化を右肩∩、右腰∪で表すとして、
- a ◁i b = (a∪
i b∪)∩
が成立する。これは、確率的アレンジメントのときも同様な等式が成立する。
復圏においてもラムダ射のアレンジメント代数においても、射のヘッジ〈hedge〉を作れる。ヘッジ自体は復圏やアレンジメント代数の構成素ではないが、中間構文として意味がある。ヘッジと射の結合は再び射になる。