デジタルデータがもうなくて、紙に印刷した絵だけ残っていたからスキャンした。いつ頃かは分からない。2013リリースのブログシステムhugoの分類システム〈taxonomy system〉がこんな感じだった気がする。
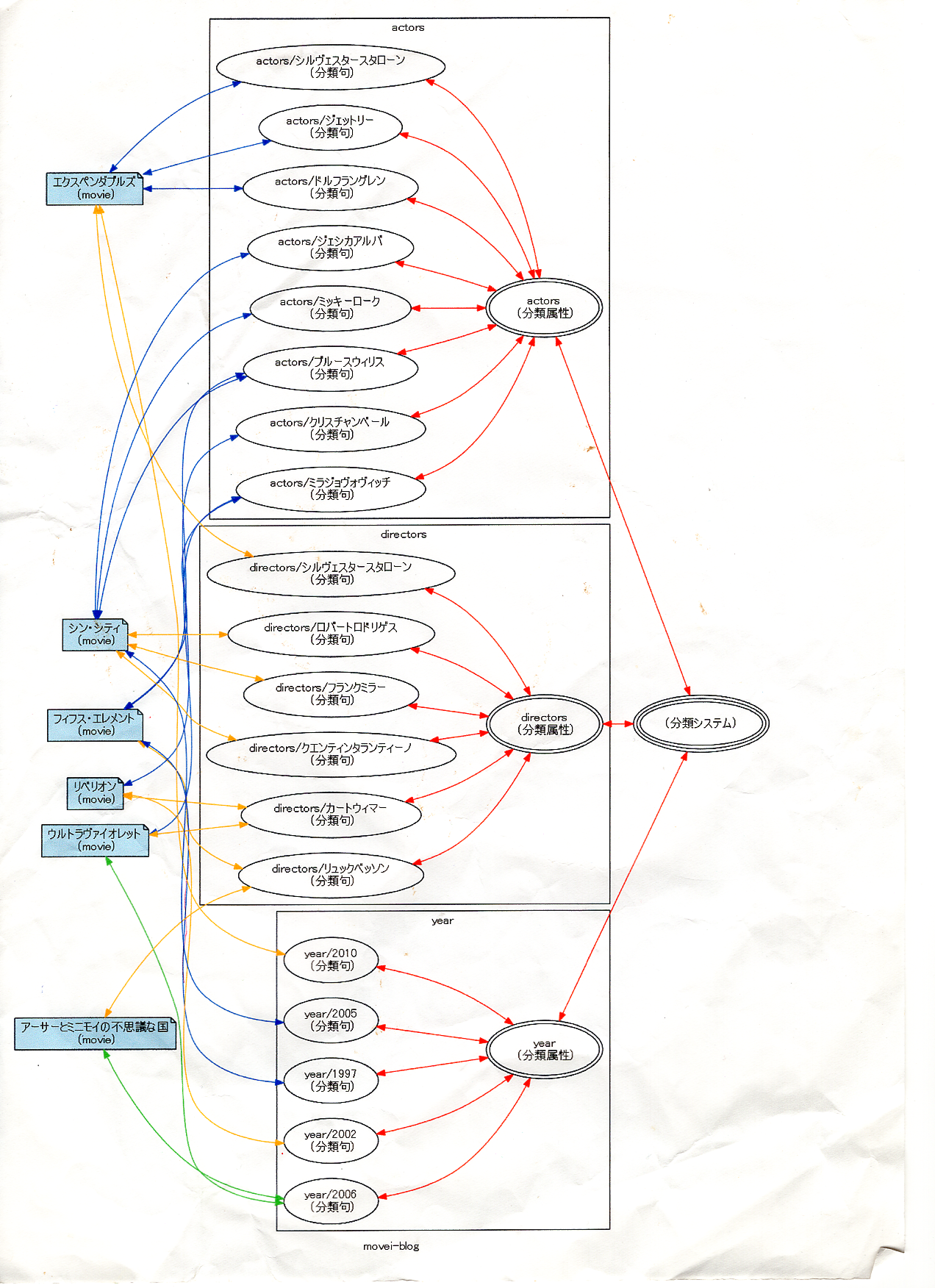
デジタルデータがもうなくて、紙に印刷した絵だけ残っていたからスキャンした。いつ頃かは分からない。2013リリースのブログシステムhugoの分類システム〈taxonomy system〉がこんな感じだった気がする。

3月28日記事 誤訳だろうが定着すれば立派な日本語 - 檜山正幸のキマイラ飼育記 (はてなBlog) にて:
ちなみにに、僕は新型コロナ禍には悲観的(より正確には反楽観的)想定をしていて、「この夜はなかなか明けないだろう」と思っています。
もちろん、自分の悲観的予測が「思い過ごしだった」となることを希望しているけど、今はこの前提で考えている。
E3 はR3と同型なアフィン空間で、大域座標を持つ多様体。内積も持つのでリーマン多様体。座標は、内積を保存する大域線形座標を使うが、それでも座標の選び方は多様性がある。
曲面は、E3の部分集合〈点集合〉だと考える。付点曲面〈pointed surface〉とは、曲面 S と一点 p の対 (S, p) 。
付点曲面 (S, p), (S', p') の局所同型は、pのユークリッド近傍 U⊆E3, p'のユークリッド近傍 U' があり、ユークリッド運動 m によって、m(p) = p', m(S∩U) = S'∩U', S∩U と S'∩U' は(集合として)同型 となること。
ユークリッド空間E3内の付点曲面は、この同型によって分類されて、その同型類は局所曲面と呼ぶ。
ジャームレベルで分類すると、無限小局所曲面になる。
このテの議論は、同値関係、同値分類、同値類、代表元 の枠組みで考えないと混乱する。
関数やセクションに関して、次の言葉を使う。
同義語をまとめると
無限小近傍でないと定義できない概念
無限小近傍に関する記述は、ジャームに関する記述になる。
Haskell演算には、加減乗除(+, -, *, /)、累乗(整数の^と実数の**)、余り mod がある。これを例とする。
セクション記法
CoqのNotation宣言
変数名(A, B)と演算子記号を含む文字列に意味を割り当てる。
変数を無名ラムダ変数にして、簡易ラムダ記法(関数記法)に使う。
演算子記号の記法情報〈notatinal information〉が事前にあるときは、無名ラムダ変数を省略してよい。
記法情報とは:
多様体Mと任意の部分集合S(空でもよいし、Mでもよい)のペア (M, S) を染み付き多様体〈stained manifold〉と呼ぶ。
(M, S), (N, T) を2つの染み付き多様体として、fはS上のN値ジャームとする。S⊆U⊆openM であるUからの局所写像 U→N の同値類がジャーム。ジャームは、S→N という写像を定義する。これをジャームの芯〈core〉と呼ぶ。芯は染みS上で定義された関数。f(S) は、fの芯によるSの像として、f(S)⊆T を満たすジャームを、染み付き多様体の準同型射とする。
f:(M, S)→(N, T), g:(N, T)→(M, S) があって、芯 f|S, g|T が集合の同型を導くとき、染み同型と呼ぶ。染み付き多様体の圏の染み同型類をグリフ体〈glyfold〉と呼ぶ。
任意の多様体の空部分集合は空グリフ体を定義し、(M, M) は全域グリフ体=多様体になる。よって、グリフ体の圏は多様体の圏を部分圏として含む。
スタッフ〈stuff〉はモノ〈thing〉とか構成素〈constituent〉と同じ。構造は、スタッフと性質からなる。性質は公理で定義される。性質を持つ⇔公理を満たす、性質を持つ⇔定理を満たす。公理は条件〈condition〉制約〈constraint | 拘束〉ともいう。
忘却関手は、スタッフを捨てるもの、公理・条件・制約を忘れるものがある。公理を忘れてもスタッフは残るが、スタッフを捨てると関与している公理も捨てざるを得ない。
構造を構成するスタッフは、圏の射(0-射=対象含む)のことが多い。射であるスタッフが所属する圏を、そのスタッフのアビタ〈habitat〉と呼ぶ。
多様体MのRkファイバーの自明バンドルに対して、任意の開集合上で共変微分が定義できる。その共変微分を"D"という記号で表すとして、それの定義を半形式的に、例えば次のように書く。
ちなみに、多様体M上の共変微分は、バンドルチャートを使って、自明な共変微分との差を取る。当該共変微分と自明共変微分との差が接続係数。接続係数は、バンドルチャートの被覆に載ったアフィン空間層の合致族〈matching family | 整合族 | consistent family〉のはず。合致条件〈matching cndition〉はテンソル場と同じだが、遷移関数の作り方がテンソル場とは違うはず。
イマイチな感じ。問題と解法と立ち位置に分ければいいような。
さまざまな関手/オペレータと微分の表示 - 檜山正幸のキマイラ飼育記 (はてなBlog)のまとめ+α。6番から先が追加。
以下の内容をひとつの記事にまとめる。
「イントラ」の初出は、イントラ層射〈intra-spacial sheaf morphism〉層に関してちょっと - 檜山正幸のキマイラ飼育記 (はてなBlog)
インデックス圏の飾り文字は、インデックス付き圏のインデックス付き対象の圏 - 檜山正幸のキマイラ飼育記 (はてなBlog)
生成単位θを持つ自己豊饒圏Cで、
が成立する。これが成立するθを生成単位と呼ぶから、同語反復だが。
事例:
| 圏 | 生成単位 |
|---|---|
| Set | 1 |
| PtSet | 2 |
| VectK | K |
| R-Mod | R |
| VectBdl[M] | RM |
| Sh[X] | 1` |
| R-Mod-Sh[X] | R |
[θ, A]C A in C を要素・ポインター・同型と呼ぶが、ほんとに要素であるためには、Cが具象圏でなくてはならない。
生成単位対象、対象の要素/部分要素、ポインター射の関係を調べる。
左項囲み、左上付き、左下付き、下線以外の真下付きはあまり使われない。が、最近僕はよく使う。特にインデキシングは左肩、左下も使う。
括弧は、グルーピング以外に演算子記号(の一部)として使われることがある。グルーピング括弧、演算子括弧、タプル囲み記号。
他に、無記号配置演算子記法もある。二項の指数、二項とみたインデックス適用など。演算子記号+引数リストの配置形式。無記号で配置のみで演算子適用を表現することもある。配置のシリアライズ方式も問題になる。"--" = "-1-2" = "_1_2" とかで書くか。
[追記]Haskellのセクションは部分適用の記法のことだから、ここの記法は略式ラムダ構文だろう。λ(x, y)(x + y) = "- + -" [/追記]